前回の続きでB1からになります。

$$ \def\bra#1{\mathinner{\left\langle{#1}\right|}} \def\ket#1{\mathinner{\left|{#1}\right\rangle}} \def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}} $$

B1. Distinguish three-qubit states

問題

次の2つのうちのいずれかの3 Qubitの状態が与えられるので、そのどちらが与えられたのかを答えよ。操作後のQubitの状態は問わない。

$\ket{\psi_0} = \frac{1}{\sqrt{3}}(\ket{100}+\omega\ket{010}+\omega^{2}\ket{001})$
$\ket{\psi_0} = \frac{1}{\sqrt{3}}(\ket{100}+\omega^{2}\ket{010}+\omega\ket{001})$
- where $\omega = e^{\frac{2i\pi}{3}}$

解答

B問題は、Qubitの状態を見分ける問題になります。量子コンピューターにおいては、量子ビットを頑張っていじっても、直接的にはその波動関数が見えるわけではないので、何とかして測定して人間が見えるようにしてやらなければ計算した意味も全く無いという話になってしまいます。なので、状態を見分けるというのは非常に重要なタスクです。一般的にはこれは必ずしも100%の確率で状態を見分ける必要はなくて、例えばBQPという計算クラスなら、誤り確率1/3以下であればよいということになっています（何回もやれば、確率に対して指数的に正解率が上げられるので、1/3ではなくて1/2未満ならなんでも大丈夫みたいです）。しかし今回のタスクは、100%の精度でこの識別を行えというものです。

非常に難しかったです。実際に正答率もだいぶ低かったように見えます。見分けるべき状態が直交しているなら割と簡単に識別できるのですが、今回の $\ket{\psi_0}$ と $\ket{\psi_1}$ は直交していない（？） ($\braket{\psi_0}{\psi_1}=\frac{1}{3}(1+\omega^{3}+\omega^{3})=1)$)ので、すんなりとは見分けられてくれません。計算間違っていて $\braket{\psi_0}{\psi_1}=\frac{1}{3}(1+\omega^{-1}+\omega^{1})=0$ なので直交していますね…。直交しているので見分けられます。

どこから手を付けたものか悩ましいですが、識別ではなく作るのであればそれなりに簡単です。 3状態のW state $\frac{1}{\sqrt{3}}(\ket{001}+\ket{010}+\ket{100})$ に Phase shiftゲート(R1) をかければ良さそうです。1Qubit目の所に$\omega$を、2Qubit目の所に$\omega^{2}$をかければ良いので、$R1(\frac{2\pi}{3}, qs[1])$, $R1(\frac{4\pi}{3}, qs[2])$を順に適用すれば良さそうです。

ということは、その逆をすればW stateに戻るということになります。$R1(\frac{-2\pi}{3}, qs[1])$, $R1(\frac{-4\pi}{3}, qs[2])$を順に適用すれば良いです。

operation Solve (qs : Qubit[]) : Int {
    R1(-PI()*2.0/3.0, qs[1]);
    R1(-PI()*4.0/3.0, qs[2]);
    ...
}

これを適用した時点で、$\ket{\psi_0}$、$\ket{\psi_1}$はそれぞれ

$$\frac{1}{\sqrt{3}}(\ket{100}+\ket{010}+\ket{001})$$

$$\frac{1}{\sqrt{3}}(\ket{100}+\omega\ket{010}+\omega^{-1}\ket{001})$$

になります。ここからさらに $\ket{\psi_0}$の方をゼロ状態$\ket{000}$に戻す操作を考えます。ゼロ状態からW stateを作る操作は、前回のA1の測定を使わない方の解をちょっといじって、

operation W3 (qs : Qubit[]) : Unit {
    Ry(ArcCos(Sqrt(2.0/3.0))*2.0, qs[0]);
    (ControlledOnInt(0, H))([qs[0]], qs[1]);
    // 1/sqrt(3)*(|000>+|010>+|100>)
    (ControlledOnInt(0, X))(qs[0..1], qs[2]); // |000> -> |001>
    // 1/sqrt(3)*(|001>+|010>+|100>)
}

このような操作になるので、W stateを元に戻すには、これの逆操作を行えば良いということになります。量子ゲートはすべてユニタリー行列であり、ユニタリー行列は随伴行列が逆行列になる行列なので、自明な逆操作が存在します。なので、一つずつ逆操作を逆に適用していけば良いのですが、そういうのはそれこそ自明に存在しているので、Q#にはその逆操作を自動で作ってくれる機能があります。

operation W3(qs: Qubit[]) : Unit {
    body(...) {
        Ry(ArcCos(Sqrt(2.0/3.0))*2.0, qs[0]); // (1)
        (ControlledOnInt(0, H))([qs[0]], qs[1]); // (2)
        (ControlledOnInt(0, X))(qs[0..1], qs[2]); // (3)
    }
    adjoint auto;
}

全体をbody(...){}で囲んで、最後にadjoint auto;と書けば、随伴バージョンを自動で作ってくれます。Adjoint F(q) などと書けば、随伴バージョンを呼び出すことができます。これを用いると、

operation Solve (qs : Qubit[]) : Int {
    R1(-PI()*2.0/3.0, qs[1]);
    R1(-PI()*4.0/3.0, qs[2]);

    Adjoint W3(qs);

    ...
}

これで$\ket{\psi_0}=\frac{1}{\sqrt{3}}(\ket{100}+\omega\ket{010}+\omega^{2}\ket{001})\Longrightarrow\ket{000}$ の変換ができました。

このとき、$\ket{\psi_1}$の方がどう変換されているのか計算してみると、

$$\frac{1}{\sqrt{3}}(\ket{100}+\omega\ket{010}+\omega^{-1}\ket{001})$$

$$\Longrightarrow\frac{1}{\sqrt{3}}(\ket{100}+\omega\ket{010}+\omega^{-1}\ket{000})\tag{Adjoint (3)}$$

$$\Longrightarrow\frac{1}{\sqrt{3}}(\ket{100}+\omega\ket{0}\frac{1}{\sqrt{2}}(\ket{0}-\ket{1})\ket{0}+\omega^{-1}\ket{0}\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})\ket{0})\tag{Adjoint (2)}$$

$$=\frac{1}{\sqrt{6} } ( (\omega+\omega^{-1} )\ket{000}-(\omega-\omega^{-1})\ket{010}+\sqrt{2}\ket{100})$$

$$ \Longrightarrow\frac{1}{\sqrt{6} } ( (\omega+\omega^{-1} )(\cos( {\cos^{-1}{\sqrt{\frac{2}{3}} } } ) )\ket{0}+\sin( {\cos^{-1}{\sqrt{\frac{2}{3}} } } ) ) \ket{1} )\ket{00}\\ +\sqrt{2}(\sin( {\cos^{-1}{\sqrt{\frac{2}{3}} } } ) )\ket{0}-\cos( {\cos^{-1}{\sqrt{\frac{2}{3}} } } ) )\ket{1})\ket{00}+...) \tag{Adjoint(1)} $$

めんどうなので$\ket{000}$の係数のみ計算

$$=\frac{1}{\sqrt{6} }( (\omega+\omega^{-1} )\sqrt{\frac{2}{3}}\ket{000}+\sqrt{2}(\sqrt{1-{\frac{2}{3}} } ) )\ket{000}+...)$$

$$=\frac{1}{\sqrt{6}}(-1\ket{000}+1\ket{000}+...)$$

$$=\frac{1}{\sqrt{6}}(0\ket{000}+...)$$

なぜか$\ket{000}$の係数が0になりました（なんでこんな都合良く0になるんでしょう？）。ともかく、これで入力が$\ket{\psi_0}$のときは100%の確率で$\ket{000}$になって、入力が$\ket{\psi_1}$のときは100％の確率で$\ket{000}$以外になる操作が書けました。

よって、これらを組み合わせて、解答が得られます。

operation Solve (qs : Qubit[]) : Int {
    R1(-PI()*2.0/3.0, qs[1]);
    R1(-2.0*PI()*2.0/3.0, qs[2]);

    Adjoint W3(qs);

    if (M(qs[0]) == Zero && M(qs[1]) == Zero) {
        return 0;
    } else {
        return 1;
    }
}

operation W3(qs: Qubit[]) : Unit {
    body(...) {
        Ry(ArcCos(Sqrt(2.0/3.0))*2.0, qs[0]);
        (ControlledOnInt(0, H))([qs[0]], qs[1]);
        (ControlledOnInt(0, X))(qs[0..1], qs[2]);
    }
    adjoint auto;
}

B2. Not A, not B or not C?

問題

以下のA,B,Cいずれかの状態が入力として与えられる。

$\ket{A}=\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})$
$\ket{B}=\frac{1}{\sqrt{2}}(\ket{0}+\omega\ket{1})$
$\ket{C}=\frac{1}{\sqrt{2}}(\ket{0}+\omega^{2}\ket{1})$
- where $\omega = e^{\frac{2i\pi}{3}}$

これらは直交ではないので確実に識別することはできない。なのでその代わりに、どの状態ではない、言うことを示せ。すなわち、

$\ket{A}$ であれば、1か2
$\ket{B}$ であれば、0か2
$\ket{C}$ であれば、0か1

を、それぞれ返せ。

言い換えると、$\ket{A}$ でないのならば0を、$\ket{B}$ でないのならば1を、$\ket{C}$ でないのならば2を、それぞれ返すというのと同値である。

プログラムは1000回実行され$\ket{A}$, $\ket{B}$, $\ket{C}$は等確率で選ばれる。操作後のQubitの状態は問わない。

解答

これが最難問のようです。いろいろ論文をサーベイしてみたところ、確かにこの3状態ならば、100%の確率で3つのうちどれかの状態ではないということが言えるみたいですが、実際に量子ゲートの形で実装できるように書いてくれているものが見つけられませんでした。

制限時間内に正解できなかったので、他の人の解答を見たところ、

operation Solve (q0: Qubit) : Int {
    mutable m = 0;
    H(q0);
    S(q0);
    using(q1 = Qubit()){
        Controlled Ry([q0],(2.0*ArcCos(1.0/Sqrt(3.0)), q1));
        H(q0);
        set m = ResultAsInt(MultiM([q0, q1]));
        Reset(q1);
    }
    if (m == 1) {
        return 1;
    } elif (m == 0) {
        return 2;
    } else {
        return 0;
    }
}

思ったよりシンプルにできるみたいです。ちなみに、MultiMはQubitをまとめて測定する関数で、ResultAsIntは計測結果を2進数でIntにデコードする関数です。

なんでこれで答えが得られるのか、実際に計算してみると、$\ket{A}$は、

$$\ket{A}=\frac{1}{\sqrt{2}}(\ket{00}+\ket{10})$$ $$\Longrightarrow\ket{0}\tag{H(q0)}$$ $$\Longrightarrow\ket{0}\tag{S(q0)}$$ $$\Longrightarrow\ket{00}\tag{Qubit増やす}$$ $$\Longrightarrow\ket{00}\tag{Controlled Ry}$$ $$=\frac{1}{\sqrt{2}}(\ket{00}+\ket{10})\tag{H(q0)}$$

$\ket{B}$は、

$$\ket{B}=\frac{1}{\sqrt{2}}(\ket{0}+\omega\ket{1})$$

$$\Longrightarrow\frac{1}{\sqrt{2} }(\frac{1}{\sqrt{2} }(\ket{0}+\ket{1} )+\omega\frac{1}{\sqrt{2} }(\ket{0}-\ket{1} ) )\tag{H(q0)}$$

$$=\frac{1}{2}( (1+\omega)\ket{0}+(1-\omega)\ket{1} )$$

$$\Longrightarrow\frac{1}{2}( (1+\omega)\ket{0}+i(1-\omega)\ket{1} )\tag{S(q0)}$$

$$\Longrightarrow\frac{1}{2}( (1+\omega)\ket{00}+i(1-\omega)\ket{10} )\tag{Qubit増やす}$$

$$\Longrightarrow\frac{1}{2}( (1+\omega)\ket{00}+i(1-\omega)\ket{1}(\cos(\cos^{-1}(\frac{1}{\sqrt{3} } ) )\ket{0}-\sin(\cos^{-1}(\frac{1}{\sqrt{3} } )\ket{1} ) ) ) \tag{Controlled Ry} $$

$$=\frac{1}{2}( (1+\omega)\ket{00}+i(1-\omega)\ket{1}(\frac{1}{\sqrt{3}}\ket{0}-\sqrt{\frac{2}{3}}\ket{1}))$$

$$\Longrightarrow\frac{1}{2}( (1+\omega)\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})\ket{0}+i(1-\omega)\frac{1}{\sqrt{2}}(\ket{0}-\ket{1}) (\frac{1}{\sqrt{3}}\ket{0}-\sqrt{\frac{2}{3}}\ket{1}))\tag{H(q0)}$$

面倒なので$\ket{10}$の係数だけ抜き出し

$$(1+\omega)\frac{1}{\sqrt{2}}+i(1-\omega)\frac{1}{\sqrt{2}}\frac{1}{\sqrt{3}}$$

$$=(1+\cos(2\pi/3)+i\sin(2\pi/3))\frac{1}{\sqrt{2}}+i(1-\cos(2\pi/3)-i\sin(2\pi/3))\frac{1}{\sqrt{2}}\frac{1}{\sqrt{3}}$$

$$=(1-\frac{1}{2}+i\frac{\sqrt{3}}{2})\frac{1}{\sqrt{2}}+i(1+\frac{1}{2}-i\frac{\sqrt{3}}{2})\frac{1}{\sqrt{2}}\frac{1}{\sqrt{3}}$$

$$=\frac{1}{2\sqrt{2}}+i\frac{\sqrt{3}}{2\sqrt{2}}+i(\frac{\sqrt{3}}{2\sqrt{2}}-i\frac{1}{2\sqrt{2}})$$

$$=0$$

なぜか$\ket{10}$の係数が0になります。$\ket{C}$の計算は面倒なので省略しますが、こちらは同様に$\ket{00}$の係数が0になります。

なので、たしかにこれを計測した結果が

$00$なら$\ket{C}$ではない
$10$なら$\ket{B}$ではない
$01$か$11$なら$\ket{A}$ではない

ということがわかるので、確かに問題が解けています。しかしこれは…どうやって導くのでしょう？？？(´･_･`)？？？

自力で解けないと悔しいので、なんとか自力で解いてみます。

1 Qubitしかなければ測定結果は2通りしか得られず、$\ket{A}$, $\ket{B}$, $\ket{C}$は直交ではないので、おそらく少なくとも1 Qubitの追加Qubitが必要になるはず（そうじゃなかったら少なくとも1つは確実に識別できてしまう）です。そこで、次のような量子回路が作れたならば、問題が解けたと言うことになります。

f:id:tanakh:20190310040114j:plain

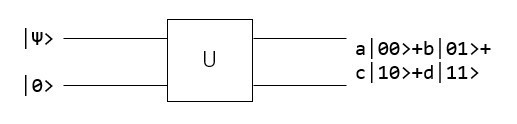
$$if \ket{\psi}=\ket{A} \Rightarrow a=0, b=0, \neq0, d\neq0$$ $$if \ket{\psi}=\ket{B} \Rightarrow a\neq0, b\neq0, c=0, d\neq0$$ $$if \ket{\psi}=\ket{C} \Rightarrow a\neq0, b\neq0, \neq0, d=0$$

ブッロホ球上でのベクトルの回転を考えると、RxとRyの合成があれば任意の回転が表現できるはずで、あとはコントロールするビットと符合の組み合わせが計4通り、トータルで8個のゲートを繋いだもので任意の記述可能なユニタリー行列は表現されるはずです（具体的な8個は後のコードを参照）。

パラメーターをdouble 8個にまで落とせたら、もう解けそうですね。そうです、焼きなましです。焼きなましに持ち込んでやればこっちのもんです。解けない問題はありません。

基本的には上の条件にマッチするときに0になって、そこから外れれば外れるほど大きくなるスコアを設定して焼き鈍せば良いですが、今回は誤差0に限りなく近い解が必要なので、温度に応じてパラメーターの変動率を下げていくのが良いでしょう。

そうして得られたのが次のコードです（先頭にH(q0)が挟まっているのはこれがないと上手く収束しなかったからなんですが、本当は無しでも行けるはず…？）。

operation Solve (q0: Qubit) : Int {
    mutable m = 0;
    using (q1 = Qubit()) {
        H(q0);
        (ControlledOnInt(0, Ry))([q0], (4.712388980385413, q1));
        (ControlledOnInt(0, Rx))([q0], (3.1415926535894254, q1));
        (ControlledOnInt(1, Ry))([q0], (0.4528278334939593, q1));
        (ControlledOnInt(1, Rx))([q0], (2.437018063152431, q1));
        (ControlledOnInt(0, Ry))([q1], (2.2598858459337396, q0));
        (ControlledOnInt(0, Rx))([q1], (1.7816609588202006, q0));
        (ControlledOnInt(1, Ry))([q1], (4.712388980374012, q0));
        (ControlledOnInt(1, Rx))([q1], (5.243709997732253, q0));

        set m = ResultAsInt(MultiM([q0, q1]));
        Reset(q1);
    }

    if (m == 0 || m == 1) {
        return 0;
    } elif (m == 2) {
        return 1;
    } else {
        return 2;
    }
}

というわけで、脳筋焼きなまし殴りでも解けたので、これで人の閃きに頼らなくても、古典コンピューターを使いこなす人間であれば量子コンピューターが扱えるはずなので、安心して眠れます。メタ的な話になりますが、こういうのを量子コンピューターで解いて欲しいものですね。量子コンピューターとあろうものを、人間が閃かないと使えないというのは釈然としませんもの。

B1. 別解

B1もやっぱり考えて解いてはいけない気がしてきたので、焼き鈍しでごり押してみます。

入力は3Qubitですが、3Qubitのユニタリー変換を探索するのは大変そうなので2Qubitに縮めます。これは$\ket{001}$を$\ket{110}$に変換して、3Qubit目を$\ket{0}$にしてしまえば良いでしょう。もう一つB2と違うところは、2状態の識別なので$\ket{\psi_0}\Rightarrow\alpha\ket{00}+\beta\ket{01}$、$\ket{\psi_1}\Rightarrow\gamma\ket{10}+\delta\ket{11}$と、それぞれ状態が確定できるように分離できるものを探します。

見つかったコードを貼り付けて、前処理を入れて、完成です。

operation Solve (qs : Qubit[]) : Int {
    // 前処理
    // |001> => |110>
    CNOT(qs[2], qs[0]);
    CNOT(qs[2], qs[1]);
    CCNOT(qs[0], qs[1], qs[2]);

    let q0 = qs[0];
    let q1 = qs[1];

    // 焼きなましで求めた2qubitのユニタリー変換
    H(q0);
    (ControlledOnInt(0, Ry))([q0], (0.000000000018460788453467103, q1));
    (ControlledOnInt(0, Rx))([q0], (5.064392436516295, q1));
    (ControlledOnInt(1, Ry))([q0], (2.324596181147987, q1));
    (ControlledOnInt(1, Rx))([q0], (4.7123889803884005, q1));
    (ControlledOnInt(0, Ry))([q1], (3.416645503599746, q0));
    (ControlledOnInt(0, Rx))([q1], (2.2141724456737695, q0));
    (ControlledOnInt(1, Ry))([q1], (3.7803967560193463, q0));
    (ControlledOnInt(1, Rx))([q1], (0.7682002923185038, q0));

    let r0 = M(qs[0]);

    if (r0 == Zero) {
        return 1;
    } else {
        return 0;
    }
}

純粋関数型雑記帳

Microsoft Q# Coding Contest - Winter 2019 - その3

B1. Distinguish three-qubit states

問題

解答

B2. Not A, not B or not C?

問題

解答

B1. 別解